Yeah, it's just a TV show. Says more about the mockers really.
Spoilers Star Trek: Discovery 4x01 - "Kobayashi Maru"
- Thread starter Commander Richard
- Start date
Our made up technical speak must be consistent! We must protect our phone-baloney jobs gentlemen!
Sometimes I wonder if you have actually seen an episode of Star Trek.
It reminds me of Troi's command test and I'm convinced Burnham would have failed it. Obviously it wouldn't be an engineering problem in her case, it would be like a child rearing problem she has to send Book to fix, like a ship eating space baby, and he will definitely die if he fixes the issue.
She should have been a new admiral ranked higher than Vance. We are going to see more admirals eventually so why not ep 1?
It's the Michael Bay school of filmography, I think he invented the technique. It adds energy to otherwise static scenes, and it's extremely annoying when the discussion is actually not all that tense or could use some contemplation on the part of the audience.
It's a solution on the same level with how Burnham fixes Book's planet, she figures out an extremely easy solution no one thought of for a century despite having space flight.
I could buy the butterflies not having dilithium, assuming I can buy them even needing it for satellites which somehow didn't explode in the Burn. But, in this case, other power sources should have sufficed. Either on board fusion reactors, or power beamed from the planet's surface, or a solar array in near orbit of their sun.
They would have had the prefix codes, and some Voyager episodes make it clear shield beaming is more about knowing the shield characteristics and getting a sensor lock. Some of that implies if you can share internal sensor data it can help get around shields.
That scene has been considered a continuity violation for how Starfleet shields work for a long time now and there's no dialogue in the episode that either Scotty or Geordi learned how to beam through raised shields. But as I said, the shields work according to story need.
That's the exact same thing I thought.
It was just like Troi's command test, and Burnham 100% would have failed because she's unable to comprehend that sometimes there's just no way to save everybody.
When it happens in old Trek it is vintage and we will happily accept. However, all Trek writers must attend my Star Trek Writing Seminar for Strict Canon Adherence (STWSSCA for short) in order to write correctly. Obviously, these writers did not.That scene has been considered a continuity violation for how Starfleet shields work for a long time now and there's no dialogue in the episode that either Scotty or Geordi learned how to beam through raised shields. But as I said, the shields work according to story need.
Cool. I look forward to her learning and growing. Keeps me coming back to Discovery.
Easy: The shields were reinforced at the sides facing the giant door, leaving the rest of the ship open for transporter beams.That scene has been considered a continuity violation for how Starfleet shields work for a long time now and there's no dialogue in the episode that either Scotty or Geordi learned how to beam through raised shields. But as I said, the shields work according to story need.
Star Trek Discovery is currently the No. 3 show on Paramount+:
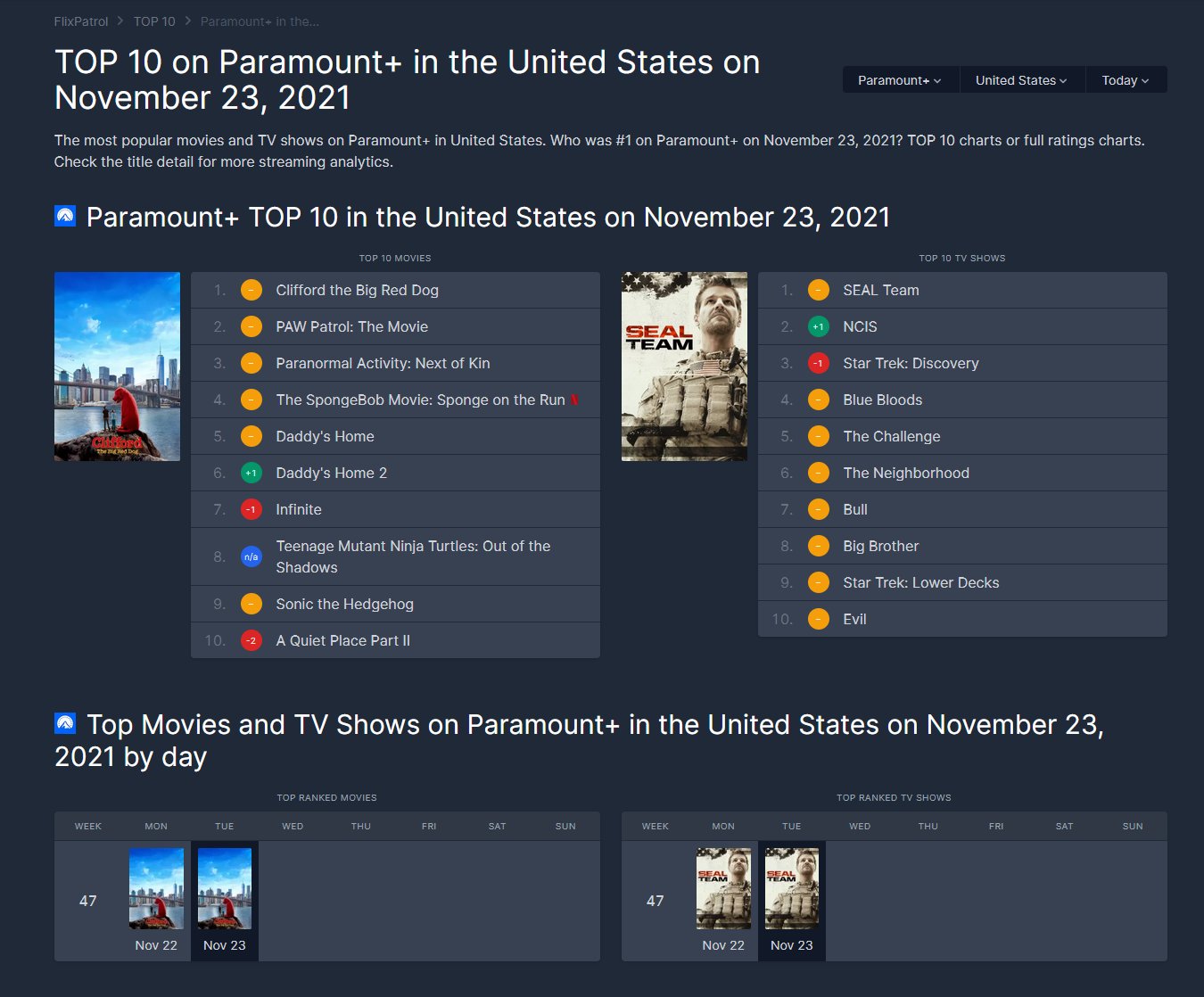
Star Trek Discovery lost its second place to NCIS.
These are not some Paramount+ exclusive NCIS episodes.
These are the already broadcasted and archived episodes of NCIS from CBS.
More people are watching old episodes from a generic, run-of-the-mill, low-budget police drama than episodes from the high-budget, high-profile, high-end (supposedly) flagship show from Paramount+.
Glass half full interpretation: 2 Star Trek shows are in the top 10.
I can't warp...factor 5.
Scotty and Geordi were beamed THROUGH shields to save their lives at the end of "Relics(TNG)," so yeah, shields work according to needs of the storyline.
Meh. 100 year old shields on the verge of collapsing.
Last edited:
I wouldn't be surprised if StarFleet had backdoor access codes to gain control of other ships within their own fleet if one should go rogue.
Well Kirk did in ST2.
And Picard with the Phoenix in The Wounded.
We also dont know if there was or was not consequences to beaming through those old shields. There may have been a Thomas LaForge and Thomas Scott that died when the ship blew up
1 6 3 0 9
Seriously. It's a weird take and quite the stretch to look at that and think it's something bad and representative of failure.
It is. At least this time having people upside down was justified, as opposed to last season’s ender, when it happened randomly and for no reason.
by whom? We’ve seen objects and beams passing through shields they know the frequencies of since forever, honestly it’s much odder when it’s not possible than when it is.
By A LOT OF PEOPLE. This is not news.
In addition to it being good that two Star Trek shows are in the top ten, I think we all need to remember something:
Star Trek has always been and will always be a niche show. It's popular enough that it's been successful for 55 years, but it's never been a #1 kind of show. Because its fundamental ethos is just not as broadly appealing.
ST isn't about the fantasy of the noble rebel who tears down repressive institutions like SW. And it's not about the fantasy of being the smartest and most powerful person who almost always does the right thing, like Doctor Who or Superman or other superheroes. And it's not a propaganda fantasy about the moral superiority of U.S. state security services restoring apollonian order against dyonesian forces of chaos like NCIS or Law & Order. It's a show that simultaneously posits that existing social structures are primitive and morally inferior and need to be torn down... AND that new structures will need to be built. It's a show about space cops exploring new planets as a paramilitary unit instead of as individualistic heroes.
This is a vision that is endearing to a lot of people, but it will probably never be a #1 show. And that's okay.
Star Trek has always been and will always be a niche show. It's popular enough that it's been successful for 55 years, but it's never been a #1 kind of show. Because its fundamental ethos is just not as broadly appealing.
ST isn't about the fantasy of the noble rebel who tears down repressive institutions like SW. And it's not about the fantasy of being the smartest and most powerful person who almost always does the right thing, like Doctor Who or Superman or other superheroes. And it's not a propaganda fantasy about the moral superiority of U.S. state security services restoring apollonian order against dyonesian forces of chaos like NCIS or Law & Order. It's a show that simultaneously posits that existing social structures are primitive and morally inferior and need to be torn down... AND that new structures will need to be built. It's a show about space cops exploring new planets as a paramilitary unit instead of as individualistic heroes.
This is a vision that is endearing to a lot of people, but it will probably never be a #1 show. And that's okay.
Amazing typo
"Geordie: For a moment I thought I was in the transporter room wall.
Scotty: Fir a moment, ye were."
Similar threads
- Sticky
- Poll
