What can we make? (no Earth)
- Thread starter evilchumlee
- Start date
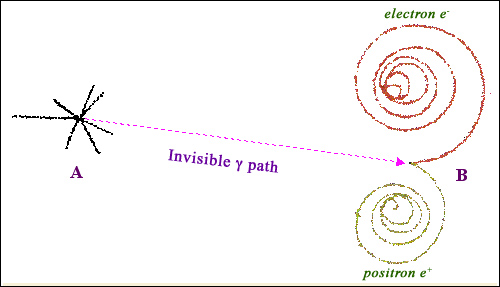
Carbon nanomaterials are degraded by ɣ beyond a certain dose. The effect is due to ionisation rather than nuclear activation. A high energy (> 10 MeV) gamma ray absorbed by a nucleus can eject nuclear particles (photodisintegration) or induce fission (photofission). For effective ɣ shielding, you need high Z materials.
www.sciencedirect.com
radioactivity.eu.com
Effect of gamma-irradiation on the mechanical properties of polyacrylonitrile-based carbon fiber
The influence of gamma-irradiation on the structure and mechanical properties of polyacrylonitrile-based carbon fibers was studied. It was observed th…
www.sciencedirect.com
Gamma Rays in Matter - radioactivity.eu.com
Gammas can travel a long way without interacting, before transmitting their energy to charged particles, usually electrons
radioactivity.eu.com
Aluminum prints just got tougher
techxplore.com
Perhaps that will help aerospace.
Things don’t look too good for NSWR
Engineers fabricate ultrastrong aluminum alloys for additive manufacturing
Purdue University material engineers have created a patent-pending process to develop ultrahigh-strength aluminum alloys that are suitable for additive manufacturing because of their plastic deformability.
Perhaps that will help aerospace.
Things don’t look too good for NSWR
I think the ultimate goal for us as people / species / or even Sci-Fi / or Star Trek is to make a "Banks Orbital".
That's the right size of Mega Structure IMO.
Not too crazy like a "Dyson Sphere" or "Dyson Ring".
Far more grand than a "Halo Ring".
Definitely achievable with Star Trek level tech.
The Overview Effect shows how large of a "Banks Orbital" we would need to construct to mirror Earth's characteristics.
For a Earth-Type Banks Orbital, you would need to meet this criteria:
For 1 Rotation in 24 hours:
- Your Inner Diameter needs to be: 3,708,676 km
- Spin Gravity will be = 1.0g
- Your Tangential Velocity would be = 485,611 kph
Tilt the Earth-Type Banks Orbital 1-2 degrees off the ecliptic plane and you have yourself a natural shadow for half the ring to produce a Day/Night cycle.
That's the right size of Mega Structure IMO.
Not too crazy like a "Dyson Sphere" or "Dyson Ring".
Far more grand than a "Halo Ring".
Definitely achievable with Star Trek level tech.
The Overview Effect shows how large of a "Banks Orbital" we would need to construct to mirror Earth's characteristics.
For a Earth-Type Banks Orbital, you would need to meet this criteria:
For 1 Rotation in 24 hours:
- Your Inner Diameter needs to be: 3,708,676 km
- Spin Gravity will be = 1.0g
- Your Tangential Velocity would be = 485,611 kph
Tilt the Earth-Type Banks Orbital 1-2 degrees off the ecliptic plane and you have yourself a natural shadow for half the ring to produce a Day/Night cycle.
I calculate the tangential velocity v to be 134.874 km/s from v = √(ra), where the radius of the orbital r = 1.854338x10^9 m (half the diameter) and the centripetal acceleration a is 9.81 m/s² . Perhaps you used the diameter instead of the radius and neglected to divide the result by 1,000 to obtain km/s from m/s?
Anyway, we should perhaps try building a Bishop ring first. As originally proposed, such a habitat would have a radius of 1,000 km and a width of 500 km, providing an inner surface area of π million km²- just less than the area of India (3.287 million km²). The tangential velocity for 1g acceleration would be 3.13 km/s.
The tensional stress σ in a rotating thin ring is given by σ = v²ρ, where ρ is the density of the ring material.
For a Banks orbital with density of 1.4, 2 or 8 x 10³ kg/m³ (equivalent to Kevlar, carbon fibre and steel respectively), the stress in the ring is 2.5, 3.6 and 14.4 GPa respectively. Those materials will fail beyond 1.0, 0.75 and 0.9 GPa respectively, so it's a similar problem to a space elevator, which requires a tensile strength of 50 GPa. Carbon nanotubes, which have a tensile strength of about 60 GPa and a density similar to Kevlar, would do the trick, but you're going to need a lot of carbon, and mass production of vast sheets of it that are potentially millions of kilometres long, not to mention finding a way to wrangle and bind them without losing strength.
For a 1,000 km radius Bishop ring, the stress in the ring to provide 1g centripetal acceleration is about 43 times less than for a Banks orbital, so the choice of construction material can be more varied, but it's still a heck of an engineering challenge. Such a ring would rotate once in 33 minutes, so you'd lose the Earth-equivalent day-night cycle.
It's probably much easier to build thousands of O'Neill habitats than a single huge ring, and these would also provide more redundancy against failure.
Last edited:
I was using the original YT video author's numbers, I didn't double check his math.
Of course we go with small steps, but as a end goal, the Banks Orbital should be a "Long Term Aspirational Target".
I don't disagree on the "thousands of O'Neill Cylinders" being more redundant.
So we'll have to wait until the Star Trek level Material science exists with far superior materials until we can achieve such feats.
Mea culpa. Both figures are correct. I misread kph as kps. My excuse is that such things are usually written in SI units and an hour is not an SI unit.
We can make small quantities of carbon nanotubes and graphene, so we have a strong enough material. Sourcing enough carbon, scaling up production and engineering its deployment are the main difficulties if one ignores the elephant in the room - that the political will to build even such structures as O'Neill cylinders will likely never exist.
KPH isn't a SI unit?
Apparently, one way to write it is "Official", the other ways aren't.
(SI symbol: km/h; non-SI abbreviations: kph, km/hr)
The history of the abbreviations:
1889: "k. p. h."
1895: "km:h"
1898: "km/h"
1899: "km./hr."
1900: "kms./hr."
1902: "k.m.p.h."
1903: "KMph."
1910: "km ph"
1911: "K.P.H."
1914: "km. hr."
1915: "km/hour"
1915: "km.-hr."
1916: "km. per hour"
1921: "kms/hr."
1922: "Kmph"
1927: "kmph."
1933: "KPH"
1939: "kmph"
1940: "KMPH
Different futures with different worlds & different political needs.
I'm sure there will be a future world that would have the political will to pull it off.
Last edited:
The SI states explicitly that unit symbols are not abbreviations, so a correct usage would be km/s. The use of h for hour is allowed by the CIPM (International Committee for Weights and Measures), but it is not an SI unit per se.
Anyway, the magnitude of the tangential velocity - about 0.045% of c - would be equivalent to 28.4 AU (astronomical units) per year, which is nearly eight times as much as Voyager 1's speed out of the solar system. One could launch deep space probes simply by dropping them off the edge. Landing on the orbital would also be very tricky as one would have to match this velocity. Leaving the orbital would similarly require extreme braking. The rotational energy in the structure would be enormous so spinning it up would need a stupendous effort that I won't bother calculating.
Anyway, the magnitude of the tangential velocity - about 0.045% of c - would be equivalent to 28.4 AU (astronomical units) per year, which is nearly eight times as much as Voyager 1's speed out of the solar system. One could launch deep space probes simply by dropping them off the edge. Landing on the orbital would also be very tricky as one would have to match this velocity. Leaving the orbital would similarly require extreme braking. The rotational energy in the structure would be enormous so spinning it up would need a stupendous effort that I won't bother calculating.
That's true, you're quite likely to see litre (L) and particularly electronvolt (eV) used in scientific literature. Pascals are generally preferred to bars as units of pressure, I would think, and I don't recall ever seeing hour or tonne used. However, provided people don't use furlongs per fortnight, a small set of derived units seems harmless enough.
Depends on the field and where you're at.
Personally, I prefer to use industry specific units.
In Aviation, we measure our speed in Knots & Altitude by Flight Level in Feet.
And the vast majority of Aviation still uses "Flight Level" around the world.
In Maritime use, they also use "Knots" for speed.
In the FireArms world, we measure mass via "Grains" & measure Kinetic Energy via ft-lbs or FPE (Foot Pounds Energy), especially since we measure Muzzle Energy by FPE.
Same with any industry that has their own specific units that don't necessarilly conform to Metric.
For Residential Real Estate Land area, dividing residential parcels down to 1 Acre is far more reasonable than 1 Hectare.
And if you're dealing with aliens, I doubt they'll be using our Metric System unless they join the UFP.
And even when they do, they'll be like us Americans with a Dual System of Measurement.
I doubt the Vulcans will have a exact Metric System that is 1:1 with ours or anything close.
But as a member of the UFP, they can more than happily have a "Dual System" of usage, just like we have here in the USA =D
I'm sure every single UFP member will go through the exact same thing and end up in a "Dual System" so we can have proper commerce & a common langue of Measurement to work with.
Last edited:
The UK also has such a confounding melange of usage, due to nimby old fartage. Metric is much simpler than the Imperial or US systems, which don't agree on things such as gallon and ton. The Imperial system also possesses units that the US one does not, such as stone (14 lbs) and hundredweight (112 lbs).
While we're on about non-standard units, I haven't seen barns and angstroms used much recently.
While we're on about non-standard units, I haven't seen barns and angstroms used much recently.
Intel & TSMC have their latest Process Nodes for Semiconductors named after Angstroms.
Intel's will be 14A
TSMC will be A16
As for the Barn (unit), that's outside of my interests generally, so I wouldn't be using it.
As for the Metric Prefix, I do want to help expand the # of Prefixes available.
I guess marketing judged that 1.4nm and 1.6nm weren't sexy enough. The usual symbol for angstrom is Å (A with an overring), of course, and the full name spelled out is not capitalised, which is at least consistent with the newton, joule and so on. It's also spelled with an a rather than an å, as I expect entering the correct Unicode was judged to be too much to ask.
As for the Metric Prefix, I do want to help expand the # of Prefixes available.
Good luck, future science students memorising that. However, it'd be a breeze for AI.
Last edited:
I don't expect anybody to memorize it, there's no point in memorizing that far down, just let it be there so they don't have to come up with the Prefixes later on.
More importantly, it gives us on the Data Storage side more room to climb on the Data Storage totem pole, enough for several generations entire life time.
When you have aspirational Data Storage goals, you need a mountain to climb.
Storing more bits than there are atoms in the observable universe (10^82 by one estimate)? Good luck with that.
Maybe somebody one day will figure out "Sub-Atomic Storage".Storing more bits than there are atoms in the observable universe (10^82 by one estimate)? Good luck with that.
=D
If so, I'm guessing that nuclear and electronic energy levels won't allow more than a few additional orders of magnitude. Spontaneous de-excitation would be particularly problematic. Now if we could exploit parallel universes, that might allow more room to stuff our bits.
Who knows, that's somebody else's problem in the future =D.
We are still fairly early on in the Pre-Fix Mountain in terms of Data Storage.
We're in the TeraByte / TeBiByte era for a single drive.
So it'll take some time for humanity to climb higher.
Similar threads
