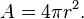Basic scientific fact... take any energy form originating from a point, and measure the strength of that relative to the distance from the point of origin, and the strength is proportional to the square of the distance from the origination point.
Which is utter bullshit, because "any energy" may easily take forms that do not obey the inverse square law or any similar law. Say, energy may be expelled in the form of individual cannonballs, which do not expand into a volume; those won't lose energy at a distance at all.
Are you serious?
You know that this law applies to, say, a neutron burst. Each and every neutron is effectively a little "canonball," and if you assume no medium through which the neutrons are passing, each neutron theoretically retains its initial kinetic energy indefinitely.
Yet the neutron field does follow the inverse square law.
Again, this is real science. And, for the most part, Trek does try to remain consistent with real science, though (as in the case of things like "soliton waves") they do occasionally come up with "perpetual motion machines" (things which violate all known laws of science, in other words), and hence are "magic."
There's nothing to say that "delta rays" would actually be spreading out into a volume and dispersing like a shower of water or ball-bearings or alpha particles, despite them originating from a point.
Yes, there is. Even a laser beam is subject to dispersion. The dispersion followed by a laser beam is a modified version of the inverse square law (the laser "dot" size is a tiny percentage of the spherical surface, but the laser still spreads out by this same law... hence a pinprick laser at the surface of the earth ends up a football-field-sized area if it hits the surface of the moon from the Earth's surface, for example).
Nothing in real science fails to follow this basic principle. "Magic"... the stuff of fantasy, not reality... might not follow this.
But as I said before, I hold that where real science CAN apply to "Treknology," it does, an we only use "pseudo-science" to fill in gaps where we have no real scientific knowledge.
So, a "soliton wave" may be utter nonsense, invented to make for a storytelling gimmick. But at least it doesn't contradict real, KNOWN science.
We know what comes from a matter/antimatter reaction, because this is real science. We've discussed the reaction-products re: this previously in this very forum, and that's what we're discussing now. So, are you claiming that there is some reaction product from a matter/antimatter reaction which does not follow the "inverse square" law?
If so, can you give us any "in-fiction" evidence to support that, at least?
Not really. It's just picking a formula and applying it outside its region of validity. Which is probably the definition of anti-science.
Absolutely not. I didn't "pick a formula." I used the correct formulae, in support of the correct theorum, which is used to describe fall-off over distance, which is EXACTLY THE TOPIC WE WERE DISCUSSING.
And it is not "outside it's region of validity." This theorum does apply to the concept of matter/antimatter reactions. If you were to toss together a gram of matter and a gram of antimatter so that both reacted fully, and you got a complete annihilation reaction, we would know just how much reaction energy was produced, by virtue of a known equation. And we would know the form that this energy would take, by virtue of real, known science. And we know that the energy density of output energy would vary by distance from that point of reaction, and that this would occur in agreement with the inverse square law as I explained it.
How, exactly, do you think that this is "outside of it's region of validity," then?
If you're measuring "temperature" as a measure of "heat energy," you're making a fatal error. These are not the same thing.
For the purposes of
this argument, temperature is the thing that matters.
No, it's not. This is BASIC THERMODYNAMICS.
For the layman, you can think of "temperature" as merely being a measure of "heat energy per unit volume." This value varies on a material-by-material basis, since the same heat energy in a given volume of one material results in a different temperature than the same heat energy in an equal volume of a different material will... this material-specific value is most commonly known as the "specific heat" or "heat capacity" of the material, in fact. "Specific heat" actually means the amount of energy required to raise a unit mass (in the SI system, that's a kilogram) by a unit temperature (in SI, that's a degree kelvin... which is the same as a degree celcius except for where "zero" is taken).
Here's a good basic table to compare some specific heat values from, by the way:
http://www.engineeringtoolbox.com/specific-heat-solids-d_154.html
Pick any two materials and compare them. Figure out how many joules of heat energy are required to bring, say, a 1 kg block of bakelite from 0C to 100C, and how many joules are required to bring an identical mass of antimony from 0C to 100C.
And then look at what happens if each block of material then comes into contact with a 1 kg mass of water (specific heat of water at 100C is 4.2159 kJ/kg K... treat this as a constant value for the sake of this calculation for simplicity's sake) and reaches equilibrium. What is the end temperature of the "antimony and water system" and the end temperature of the "bakelite and water system?"
The math here is quite simple. It's the JOULES OF ENERGY which count, not the temperature, though. All that the "delta T" affects is the rate at which the energy transfers.
Now, from the standpoint of a human body, well... we're mostly water, and so we generally use the thermal constant value of water as our yardstick by which we measure everything else.
What this means is that we may have, say, a big block of steel at one temperature (say, 200 degrees F) and an identical block of some other material (let's say polystyrene) at 200F and put both, separately, into a volume of water. The polystyrene will result in a much smaller overall effect on the temperature of the volume of water than the steel will, because the thermal constant of the steel is much higher... more heat transfer is required for a given change in temperature.
"Heat energy" is redundant anyway - heat is energy.
It is not "redundant" because while all heat is energy, not all energy is heat.
Technically, the term we use when doing science is "enthalpy"... this is the synonym for "heat energy." But I chose not to use the term "enthalpy" because few people in the general population would have any clue what I was talking about where I to have used that term, while most normal folks (with a robust intellect, even if lacking this level of scientific training) will be able to grasp the concept of 'heat energy."
You do seem to "get" this based upon your next comment, so I have to assume you're just quibbling when you object to my terminology, however.
But only the forms that make you feel hot are relevant to the nacelles-are-hot argument. And the diesel engine doesn't scorch you, while the searchlight does, because the latter ejects more of its unusable energies (or exergies, or whatever terminology you want to use) in a manner that causes an inconvenient local temperature increase.
"Exergies?" I've never cared for this term, personally... energy is energy, and redefining a new term to describe energy based upon the direction it is flowing always bothered me. That's like saying that what flows through a hose in one direction is water, but if the water flows the other direction, it's no longer water.
In fact, in general, I tend to treat this as the "entropy" of the system (entropy meaning unusable, unrecoverable energy... "disorder in the system"), though this is a bit of a stretch of the definition of entropy in general.
So, the term "unusable energy" is much clearer, I would think.
The problem with your argument, above, is that you seem to be treating "a relatively small amount of heat energy forced into a small volume where it is retained due to insulation and a high local specific heat" as somehow being more significant than "much more heat energy, dispersed int a large volume where it can easily conduct and convect away and where there is a low specific heat."
This works when dealing with a diesel generator and a search light, true. But in a starship, which is a CLOSED SYSTEM, you don't have that "infinitely large heat sink" (for the sake of calculation) of an atmosphere which we have here on Earth. You have a small, finite volume, with a very low specific heat.
Imagine it this way. Have a "tether" spacecraft with the generator in a "pod" at one end of the tether, and with the spotlight in an identical pod at the other end of the tether. Imagine that you have electrical conduction along the tether but no thermal conduction, to make it simpler.
And, also to keep things simple, ignore any elimination of the heat through radiation.
In other words... all heat generated by the generator set is retained in the first pod, and all heat generated by the lamp is retained in the second pod. Eventually, the local heat generated by each will cause a temperature rise in its respective pod.
In which pod will the overall temperature increase more rapidly?
So, let's say the warp core in the middle of the ship pumps out more heat than the end user nacelles outboard. Nothing says the nacelles wouldn't be hotter - which countermands your original deductions or assumptions.
I hope, now, that you see that this statement is untrue. "Hotter" is only relevant when viewed in terms of "stored heat energy" which is related to the heat capacity of the material whose temperature you're measuring.
When you think of it that way... a nacelle has a much higher mass-density than the inhabitable volume of the ship, with the majority of what's in the nacelle being solid mass (metal and ceramic, I presume) and the majority of the volume in the hull being atmosphere. So, for the nacelles to get hot requires a LOT more energy to be added to the system, when compared to the same temperature rise occurring in the main hull of the vessel, doesn't it?
I may have to adapt that, and with your permission, I might (no promises).
or a 
or a 
or a 
can help to show the "not so serious" intent behind a comment.
or 
or 
or 
or, as used a few lines up in this thread, 
are pretty effective communicators of "mockery."
