A Probabilities Problem
- Thread starter IndyJones
- Start date
TheLonelySquire
Vice Admiral
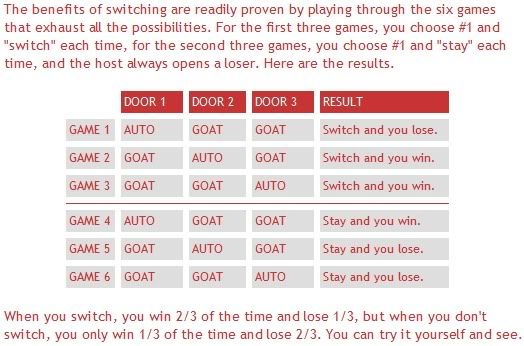
I saw this problem earlier today, and really enjoyed it. I realize it's an oldie, but had never seen it before. And I wanted to see what you guys thought of it.
Oh, and I've tweeked it to make it Trek appropriate.
So, what say you?
I say it's a 50/50 shot either way.
I know that, statistically, it ends up being better odds to switch, but I don't remember why.
ETA: Here it is; it's the Monty Hall Problem. The best explanation of why you should switch, for me, is this one:
ETA: Here it is; it's the Monty Hall Problem. The best explanation of why you should switch, for me, is this one:
The whole point of understanding probability is that it ISN'T 50/50, though. If you were being offered the choice of 2 doors, you'd be right, but the problem starts with the 3, and you had a 33% chance of picking correctly. Once you see door #3, you've got a 66% shot at door #2 instead of #1, which still only has that 33% probability...
By switching, the host offers you the chance to pick door #1, OR doors 2 and 3. Presented like that, it's a no-brainer, right?
Sure, could still be #1, but since it's dumb luck anyway, gotta play the odds.
Probability is fun like that. Like flipping a coin, and landing on heads 100 times in a row. Still 50/50 odds on the next one, but your brain wants you to either roll with the pattern, or decide it CAN'T go 101 times, and go contrary. 50/50 no matter the previous history. Yet looking from the other side of it, odds of flipping heads 100 times in a row: not so good...
Here's the solution from where I found the problem (an old Marilyn vos Savant article from a couple issues of Parade in 1990 and 1991). Apparently she had thousands of people write to tell her she was wrong, and many were PhD's and University faculty. Even after she posted the following chart, they still persisted in writing her to say how astounded they were that she continued to believe in her solution.
Finally, she asked people to actually try it and submit their results, and that's when people finally started to believe her. She really is quite bright - not shocking for a woman with an estimated IQ of somewhere between 170 and 230!
Finally, she asked people to actually try it and submit their results, and that's when people finally started to believe her. She really is quite bright - not shocking for a woman with an estimated IQ of somewhere between 170 and 230!
I've seen this puzzle and the answer before, but it wasn't until reading this thread that I understood the solution.
I was having a conversation about this the other week and I'm afraid it's still up there with some parts of relativity that my brain refuses to comprehend.
I get that when the question was first asked you have a 1 in 3 chance of being right. But once the door is opened to reveal one of the goats/Klingons, I just don't understand why picking the next door isn't a 50/50 choice.
I get that when the question was first asked you have a 1 in 3 chance of being right. But once the door is opened to reveal one of the goats/Klingons, I just don't understand why picking the next door isn't a 50/50 choice.
Why the first box retains it's probability:
Imagine if there were 1000 boxes. You pick one box and don't swap. You have a 1 in 1000 chance of winning. If you have no intention of swapping, then the other boxes do not matter. What the host does with them does not matter. The box you initially choose retains its 1 in 1000 chance of being the winning box.
Why the swap is more lucky:
The chances on all unknown boxes adds upto 1. The prize must be in one of them.
So if your box is 1 in 1000, and there is one other box where the good prize could be, then because the sum of probabilities = 1, the other box must make up the 999/1000.
Imagine if there were 1000 boxes. You pick one box and don't swap. You have a 1 in 1000 chance of winning. If you have no intention of swapping, then the other boxes do not matter. What the host does with them does not matter. The box you initially choose retains its 1 in 1000 chance of being the winning box.
Why the swap is more lucky:
The chances on all unknown boxes adds upto 1. The prize must be in one of them.
So if your box is 1 in 1000, and there is one other box where the good prize could be, then because the sum of probabilities = 1, the other box must make up the 999/1000.
This is the explanation that makes the most sense to me. (EDIT--I posted this before I read Jadzia's explanation)
If offered the choice between opening two doors, or just one, I would certainly choose two. I might still lose, of course, but intuitively, I would seem to be doubling my chances of winning.
But the way the puzzle is actually presented, my intuition also tells me that there should be no difference between switching and standing pat. I get to see what's behind two out of three doors, either way.
So this seems to be an even more interesting problem of psychology. The puzzle is presented in such a way that it takes advantage of a weakness in intuitive probability or "folk probability." But where does this weakness come from?
This "solution" is incorrect. Despite the rigamarole, at the end, you're still left with 2 doors. One contains the prize the other contains the goat. It's still 50-50.
Yeah, it's unlikely that you picked the correct door to begin. Your odds of doing so at the outset are 1 in a million. Conversely, it's also 1 in a million that the other door contains the prize at the outset. However, as other doors open and you gain more information, the odds for your door increases to 1 in 2. The odds for the other door also increases to 1 in 2.
This is the new decision point: 1 in 2 for one door and 1 in 2 for the other. It's a coin toss at that point.
Mr Awe
You mean, intuition in the philosophical sense? The sense in which I used it?
I seriously doubt it. That would be like trying to measure love.
Do you have any suggestions?
You were asking where it came from and I was asking how it could be measured, whatever 'it' is.
I understand. I replied, 'no, I don't think so,' and asked if you had any suggestions on how to do so.
Mr Awe -- the boxes are not symmetric though. If they were, say if you were approaching the game at the two box stage and had no clue which was initially chosen, then it would be symmetric, and it would be 50-50..
The asymmetry is this: One box is a blind choice of 1 in 1,000,000. The other box has been selectively whittled down from a larger set. That isn't random. It has been fail boxes that have been removed. Each fail box removed makes that set of 'others boxes' more and more lucky.
In the three box game, you know which two boxes has been selectively whittled down to one, and you know which box is the blindly chosen one.
The asymmetry is this: One box is a blind choice of 1 in 1,000,000. The other box has been selectively whittled down from a larger set. That isn't random. It has been fail boxes that have been removed. Each fail box removed makes that set of 'others boxes' more and more lucky.
In the three box game, you know which two boxes has been selectively whittled down to one, and you know which box is the blindly chosen one.
^Like I was saying: folk probability vs. mathematical probability.
Actually, now that I think about it, I can think of a case where a scientist tried to roughly measure his colleagues' intuitions. Before he performed his obedience experiments, Stanley Milgram asked various experts to predict what percentage of his experimental subjects would continue to obey orders to the end. Most experts predicted that only a very low percentage would do so. But in fact, the percentage was very high.
Social psychologists use this an example of fundamental attribution error--our (mistaken) intuition that character matters more than circumstance in determining people's behaviour.
Actually, now that I think about it, I can think of a case where a scientist tried to roughly measure his colleagues' intuitions. Before he performed his obedience experiments, Stanley Milgram asked various experts to predict what percentage of his experimental subjects would continue to obey orders to the end. Most experts predicted that only a very low percentage would do so. But in fact, the percentage was very high.
Social psychologists use this an example of fundamental attribution error--our (mistaken) intuition that character matters more than circumstance in determining people's behaviour.
You're confusing probablity of choosing the right value, with possibility of outcomes.
Here's how I see it:
You see it as always 50/50, as you only have two values - prize, or no prize.
The probability of choosing the correct value at the start is always 1/3, as the prize could be in any one of the 3 choices.
At this point, there are three possible outcomes:
You have the prize.
One other door has the prize.
The third door has the prize.
Then one unchosen door is opened (either the second or third), showing no prize. Now the possible outcomes are:
You have the prize. The unopened door also has no prize. Switching now means you will LOSE.
You have no prize. The door that has opened has no prize. The unopened (3rd) door has the prize.
You have no prize. The third door that has opened has no prize. The unopened (2nd) door has the prize.
In the latter two situations, switching means you will WIN. In other words, now that you have the extra information that one of the other doors has not got the prize, you are left with two winning situations out of three if you choose to switch, but only one winning situation out of 3 if you stick. Thus, by switching, the probability of choosing the winning outcome = 2/3
Similar threads
