Questions Regarding The Universe

[Shaw]

... what Iwas wondering is if there are any other closed surfaces besides spheres/hyperspheres that have been considered for our universe, or if that's the only one that would work, of if there's no way to know, etc, etc....

Most of the ones I've heard about are generally not all that interesting, like the 3-sphere (positive curvature) or 3-torus (zero curvature), and most models seem to be kept in the range of orientable manifolds.

While most models are being based on sphere and torus topologies, there are some people playing with higher dimension versions of non-orientable manifolds like the real projective plane or the Klein bottle. The Klein bottle is a pretty well known topological figure, but the real projective plane isn't nearly as popular. As it happens, the real projective plane is the topological figure that I often wrestle with as a mental exercise.

The standard immersion of the real projective plane into Euclidean 3-space is rather trivial looking...

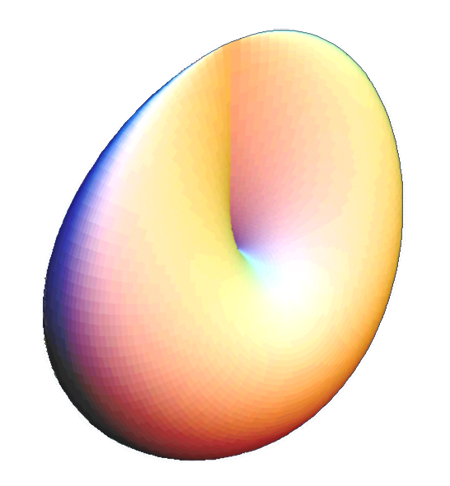
But there is a problem with this version from a differential topology point of view in that it has two points (called Whitney Umbrellas) which are non-differentiable (non-smooth). In differential topology you want smooth immersions of manifolds, and one example of such an immersion is my Avatar, which is the build up of this version...

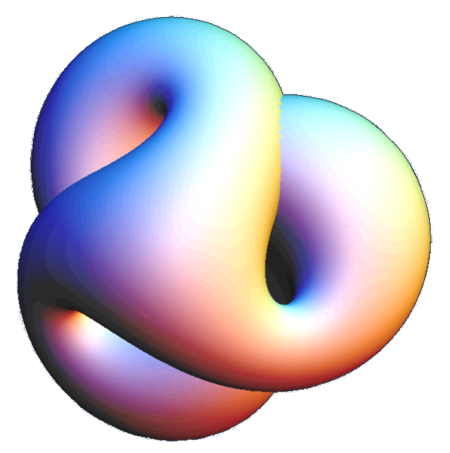
But I've always felt that you lose a lot of knowledge about these things if you just sit back and watch a computer draw it for you, so periodically I sit down with a handful of sheets of paper and from memory draw different versions of this surface, like this one I did for my wife a few years back (with further examples here)...

I have outlined a tutorial on how to create such drawings, but haven't had the time to finish it... though I hope to in the next few months.


All that might be somewhat off the topic, but without a definite answer as to the true topology of the universe, a study of a number of different topological manifolds might one day provide the insight we need.


The non-hand drawn figures were made using 3D-XplorMath.

 

[Sheliak]

"As far as the laws of mathematics refer to reality, they are not certain, and as far as they are certain, they do not refer to reality."

 

[Shaw]

"As far as the laws of mathematics refer to reality, they are not certain, and as far as they are certain, they do not refer to reality."

I've often counseled people on not mistaking the model for the subject. Mathematics is a construct of the mind, as are the models of nature we create using mathematics.

Physics is like art where you sit down and attempt to draw or sculpt a subject in greater and greater accuracy. The danger that is always present is when people mistake the mental model for nature itself... or ending up preferring the model to nature when your original goal was to study nature.

The trap is when a theory is so beautiful and elegant that those working with it are unwilling to give it up even if it prove to not model nature as we see it. Physicists and the like should always be willing to walk away from a theory if it diverges from what we know of nature.

When asked what he would have done if the eclipse experiment that was one of the first proofs of General Relativity had not proven it, Einstein jokingly said:

"Then I would have felt sorry for the dear Lord. The theory is correct."​

But here is the thing... while these models may seem disconnected from nature in that mathematics is a construct of our minds, our minds are a construct of nature. We are the universe attempting to figure out what it is, we are nature's steps towards self-realization.

History has shown time and again that pure mathematics (which was done without any thought towards application in anyway) has been found at times to be the missing pieces of some puzzle in the study of nature. Riemann's work in the mid 1800's on geometries had no natural applications until Einstein and Hilbert started work on General Relativity. Lie's work on spherical group structures in the late 1800's had no natural applications until after Yang and Mills started the area of Gauge Theories. So even when mathematics isn't attempting to model nature, it is still being created by a construct of nature, and so there is always the possibility of a link back to the study of nature.

So yeah, don't forget that what you are really studying using all that mathematics is nature... but at the same time don't forget that nature is the source of all mathematics.

 

[Sheliak]

don't forget that nature is the source of all mathematics

I disagree.

 

[Jadzia]

A question. Has there been any inroads made to to physically show the topological properties of the universe? AFAIK there has been many models proposed that is mathematically sound which is problematic in the same manner as the string theory. If not what on the theoretical horizon would offer some glimpse of hope that such endeavor is even possible?

The main issues are in figuring out the global curvature... and there doesn't seem to be (the last I heard) a straight forward way of checking the curvature.

The best analogy is the surface of either an apple or a basketball. On the large scale view of them, both are topologically a sphere... but if you were exceptionally small on the surface of either of them, their irregular shapes might keep you from seeing their large scale topology.

And one little "tunnel", would completely change that topology, turning a sphere into a torus, or a torus into a two holed torus, or worse. We have no realistic hope of ever finding these tunnels if they do exist because they could be microscopic 100000 light years away somewhere, so the topology is unknowable.

One of the ideas in topology are homotopies, and the idea of an expanding universe is that it remains homotopic to its earlier states.

But if we want a big bang, we start out with what? A point? That isn't homotopic to a sphere or a torus. So what happens to change that? There's something I find unsettling about "spatial surgery" If it is possible, then it is also possible that our universe may have some sort of schism and cleave into two disjoint universes, Similarly, two universes may blend together and suddenly we get a little window opening up into that other universe, like two bubbles fusing together.

It is possible that little bits of our universe are evaporating all of the time, like blisters on the surface of a large bubble which pull away like little bubbles. The reverse might also happen, with our universe attracting little spatial bubbles with its gravity; other microscopic universes which haven't the energy to expand, and these make little additions to our own universe.
Might this be the expansion we witness?

After all, gravitons are allegedly not constrained to the brane, else they would never escape black holes, and black holes would have no gravitational pull outside of the event horizon. So if gravitons are free to move off the brane, they are free to move off and into other universes, where they might draw those towards our own, like these little microscopic bubble universes. Big universes like our own might be too big and massive to move.

Just random thoughts here.

 

[Shaw]

Just random thoughts here.

Just to play devil's advocate here... when I see you talking about this stuff, I'm getting the impression that you are unable to leave an immersion space out of the mix.

For example, when you think of a 2-sphere (S^2), are you envisioning a standard sphere (which is an immersion mapping of S^2 into R^3)? And when you talk about bubbles moving around and touching, that sure sounds like you are envisioning a bunch of different size S^3 like manifolds immersed in some R^n... but then where is this R^n construct? What is it's nature?

The danger of thinking of immersed topological surfaces is that when you want to take them to higher dimensions, if you haven't removed the R^3 training wheels first, you end up building this vast outer construct out of habit.

If your wondering why Quantum Gravity hasn't progressed very far, it is because most everyone who has made attempts are coming from a situation where they are used to having something like R^n to work from. Similarly, I've seen a lot of rationalization done for extra dimensions which were originally just group structures rather than physical dimensions. I get the feeling that people in quantum field theories have forgotten (or might never have been taught) what a group is.

I mean, when I teach people about group theory, the concepts are really basic. A group is a set of elements with an operation and an identity element. The best example would be the set of numbers on the face of a clock under addition with "12" as the identity element. That group is similar to U(1)... would you classify the clock face group under addition as a physical dimension? Once you start getting the idea of what groups are (and are not) doesn't the fuss over treating them like physical dimensions sort of seem a little extreme? They are degrees of freedom, with particular rules, but I wouldn't feel inclined to worry about how they roll up so that they aren't seen like physical dimensions. What, after all, is the physical size of the clock face group under addition? It is an abstraction of a degree of freedom which (in the case of U(1)) doesn't actually exist within normal 4 space-time.

When I think of a torus (T^2), I think of a square where if you travel off one side you pop back in on the other. I don't see a donut shaped object because (1) that is a distortion of T^2 and (2) it is dependent on R^3. Both of those aspects can trick you into envisioning things that aren't there.

And the same is true in differential geometry. It is one thing to play with the classical differential geometry of surfaces in R^3, but at some point you have to divorce yourself from these things existing in some form of R^n and just work with strictly the intrinsic properties of manifolds. This is the heart of Riemannian Geometry and the need to understand that the intrinsic metric on a manifold is what is important.

But yeah, if you have these bubble universes moving around, they must be moving around in a higher reference frame like an R^n, which begs the question... doesn't that have to be immersed in some higher R^(n+m)?

Once you start down this path of a universe of russian dolls, you've got a real problem of where to finally draw the line... where do you stop the nested spaces?

For me, I don't let them into the picture from the start. And that is the real trick to General Relativity that is so hard to grasp for most people. Like viewing a torus in R^3, attempting to view aspects of General Relativity in some form of R^n can actually hide the important aspects.




I haven't read it myself, but I've heard from many of my professors that Flatland is an excellent starting point for understanding the limits of perceived dimensions... and understanding how limited the universe would look if it had only two physical dimensions might help with visualizing the limitation we face living in three physical dimensions. Plus I heard it is a cute story too.

 

[ITL]

Once you start down this path of a universe of russian dolls, you've got a real problem of where to finally draw the line... where do you stop the nested spaces?

"It's turtles all the way down, of course!"



Seriously, though - I can't pretend to understand a tenth of what yourself, Jadzia and others have posted, as my understanding of Relativity and Quantum Physics is still at Step One For The Layman - "Curvy Spacetime and Little Bits Of Vibrating Energy". But it's utterly fascinating stuff, nonetheless.

Rock on.

 

[Shaw]

Seriously, though - I can't pretend to understand a tenth of what yourself, Jadzia and others have posted...

I have to wonder sometimes if I'm the only person who has seen the incredible strides Jadzia has made. This type of learning curve would be awesome when done within a normal course like structure, and yet she has made these strides in virtual isolation, on her own, driven by her passion for the subject... and she is better at the math than me!

Plus I'm pretty much stuck in Classical Physics... while she has all of physics as her playground.

 

[Jadzia]

Just random thoughts here.

Just to play devil's advocate here... when I see you talking about this stuff, I'm getting the impression that you are unable to leave an immersion space out of the mix.

For example, when you think of a 2-sphere (S^2), are you envisioning a standard sphere (which is an immersion mapping of S^2 into R^3)? And when you talk about bubbles moving around and touching, that sure sounds like you are envisioning a bunch of different size S^3 like manifolds immersed in some R^n... but then where is this R^n construct? What is it's nature?

Yes I visualise these manifolds as embeddings in higher dimensional spaces.

But Russian Dolls... Well in my opinion, it depends how we interpret space and dimension. Let me explain how I do.

In order to study and measure space (and time), we need a coordinate system, so we introduce axes. The space doesn't really have axes. We just use them as a basis, and it is essentially an arbitrary construction, but done for our convenience, like cartesian, or cylindrical polars, oblate-sphericals or whatever.

Space is simply a common arena where entities have relationships. Space isn't really anything -- it the mass which is something. It is mass which has relationships with other masses. I dont really like the idea of space having some weird metric because space isn't anything. I try to visualise it all in terms of the relationships between entities. However, space is a visual construction we make and use to assist the visualisation of these relationships.

This is how I perceive space.

We introduce the idea of three dimensions because these relationships are mostly able to be described with three. But when we have the effects of relativity, three don't seem sufficient. The commonly accepted way is to introduce weird metrics and talk about spatial measures through non-euclidean geometries.

Personally, I rather introduce new dimensions which give me additional free variables to describe the relationships for which three variables are inadequate.. What relativity does is stay with just three dimensions and introduce these free variables into the metric -- so giving a weird metric.

It is like where we were talking in another post about the surface geometry on Flamm's Paraboloid being equivalent to the non-euclidean geometry of schwarzchild metric. The result is the same -- what we have is a way of describing the relationships between entities, one with a surface embedded in a higher dimensional euclidean space, one with a non-euclidean metric.

Now I'll be the first to admit, that my approach may not be correct, but this is where my mathematical intuition is strongly pulling me. Non-euclidean metrics just seem to me like a compromise, where we're forbidden from using a higher dimension, when (in my view) it is the most natural extension to our current description.

Take for example spherical geometry and how triangles have angles which add up over PI radians. Well yes, but... we're working on a sphere ... embedded in a higher dimensional euclidean space. It doesn't seem necessary to have weird metrics and a two coordinate system. Just have euclidean metrics on a three coordinate system, and impose a surface constraint.

 

[Meredith]

I want a small basement universe that I can use to give myself a back rub.

 

[Shaw]

Take for example spherical geometry and how triangles have angles which add up over PI radians. Well yes, but... we're working on a sphere ... embedded in a higher dimensional euclidean space. It doesn't seem necessary to have weird metrics and a two coordinate system. Just have euclidean metrics on a three coordinate system, and impose a surface constraint.

Okay... how do you deal with a torus then?

In the space T^2, all triangles are the same as if they were drawn in R^2, but I know of no smooth immersion mapping of T^2 into R^3 that preserves this aspect of T^2. The donut shape that one would envision in R^3 has two regions of very different curvature... an outer region of positive curvature (not unlike S^2 in R^3) and an inner region of negative curvature.

Now, imagine that you are a 2-person moving around in T^2, where the metric is Euclidean, and some 3-person comes along and decides that they want this T^2 as an nice model on their desk, so they totally distort it into a donut. What was once parallel lines in T^2 land are now completely warped, and what was once a constant metric over all of T^2 space now radically changes from place to place.

Further, when studying Riemannian Geometry these days, it is actually best to take a coordinate free approach (which you wouldn't normally see in most General Relativity texts). Most of the time when I was in school we talked about this stuff in the most abstract terms (a manifold M^n with metric g), it is just that when it comes to General Relativity people in the physics community are often more interested in concrete applications (such as the Schwarzschild solution) rather than a global understanding.

It is hard to show you how Flamm's Paraboloid with a scalar function for time dilation doesn't work because the basis of Flamm's Paraboloid is in fact a sort of flawed model. Just as in Special Relativity, when you disregard aspects of time, things stop working out correctly. The one thing that Special Relativity should teach (and everyone should remember) is that the idea of simultaneity can not be enforced as it is different for every reference frame... but Flamm's Paraboloid is an attempt to do just that.

General Relativity is sort of like gasoline, this stuff doesn't perform that well when watered down.

But think about it, isn't having to introduce Euclidean coordinates in ever greater numbers just so you can avoid an intrinsic metric more of a compromise? And isn't this construct of convenience taking on a life of it's own when you assume that (like letters jumping off a page and dancing around) gravitons could travel through this Euclidean space to another universe? This construct of convenience is the pre-existing infinite universe, even though there is absolutely no evidence of it.

I mean this outside is really sort of what I was talking about before... putting together a mathematical idea and do to comfort and esthetics disregarding nature. What started as a way to avoid non-euclidean metric becomes a medium for gravitons to jump from universe to universe even though you said space isn't really anything. That sure sounds like something to me!


Besides, we need to keep some of these spaces independent of immersions into Euclidean space so that we can set up a small T^3 space for Meredith to give herself a back rub.

 

[Sheliak]

The universe is flat and will expand forever.

 

[Ronald Held]

That is the current view, assuming the the negative pressure is due to the cosmological constant, and not some other scalar/tensor field(s) which decrease to a very low value in a finite time scale.

 

[Jadzia]

Okay... how do you deal with a torus then?

I'd factor R/~Z and imagine a bounded cube of euclidean space with a euclidean metric, with this same factoring. I wouldn't twist a space up just for the sake of it.

I'd only introduce these extra dimensions to describe relationships which cannot be described with three variables. The torus you describe doesn't need more than 3, (before relativity). It doesn't need to be twisted up and embedded in R^4 as the 3 dimensional surface of a 4 dimensional donut.

But just because mathematics can describe a nice manifold doesn't mean that space-time can form such a shape. You want something flat, yet cyclic. R/~Z is a bizarre object.

The nice property of the scwarzchild solution is that it is a steady solution, that is time independent. But admittedly, my higher dimensional description doesn't immediately give the necessary mechanics for considering motion/trajectories. But for relatively stationary observers, (relative to the star too), this method does accurately describe the spatial-temporal phenomenon they'd experience.

But think about it, isn't having to introduce Euclidean coordinates in ever greater numbers just so you can avoid an intrinsic metric more of a compromise? And isn't this construct of convenience taking on a life of it's own when you assume that (like letters jumping off a page and dancing around) gravitons could travel through this Euclidean space to another universe? This construct of convenience is the pre-existing infinite universe, even though there is absolutely no evidence of it.

The evidence is right before you The fact that three variables are not sufficient to describe relativistic space. Like I said before, it is really just a question of where you want your additional free variables to be -- as extra dimensions or as the coefficients in a non-constant metric. Take your pick. I like dimensions.

The point I tried to make in my last post is that our familiar concept of space as a measurable expanse, is only a human construct, probably influence largely by the mechanics of vision. If you think of space algebraically, solely in terms of how many variables needed to describe the relationships between particles, it breaks down the traditional notion of space, and you don't see any Russian dolls.

The point I want to communicate is that new relationships (new variables) that may emerge in our theories, are not something to frighten us. We should not think of our universe becoming infinitely extended into a new dimension because of it. The relationships are like different attitudes that matter expresses towards other matter. People do this too: There are many different ways of loving and hating; being attracted and repelled by another; and in many varying strengths. Those which are felt quickly and strongly feel nearby, while those which are slow and faint feel somehow distant. The fundamental forces are rather like that too.

In analogy, if we try and describe socio-dynamics, by charting each independent emotion via a separate dimension, we get a similar construct, if our limbic system grew as powerful as our visual cortex, we might develop a spatial perspective of emotion. But this does not mean that emotion (or indeed any 1 dimensional aspect of emotion) is literally an extended dimensional expanse.

Now this analogy isn't perfect, but I think it adequately describes the way I perceive space, enough to communicate and justify my approach.

I mean this outside is really sort of what I was talking about before... putting together a mathematical idea and do to comfort and esthetics disregarding nature. What started as a way to avoid non-euclidean metric becomes a medium for gravitons to jump from universe to universe even though you said space isn't really anything. That sure sounds like something to me!

Well the brane theory isn't my invention, it just seems compatible with my approach because of the talk about needing 21 dimensions (or whatever it is) for giving the correct string and brane behaviour.

In the view of brane theory, our space-time is something like this IIRC: It is realised as a 4 dimensional sheet floating in a higher dimensional "super-space". Other sheets may also exist floating in that super-space, and the big bang is thought of as a point where two sheets touched and recoiled, sending a ripple across both sheets.

But what I say about gravitons must have some truth -- unlike other particles they must be able to escape black holes else black holes would have no external gravity. And since gravity is just a warping of space-time, gravitons must leave space-time through another dimension. A metric would not work here.

Additionally, this extra-dimensional ability of gravitons is the general belief why gravity is an exceptionally weak force.

 

[Shaw]

My wife (who is a cook) pointed this out to me while we were discussing this... there is a point when attempting to teach someone a recipe where you see them using the wrong measurements or wrong ingredients and they seem to be doing so on purpose to make sure that the dish fails. If you know the person can cook, then maybe they hate the dish so much that no matter what, they will do whatever they can to sabotage that dish.

I seem to have been laboring under the false assumption that you wanted to learn relativity... but over and over again you have done things like removing time (which relativity without time is not relativity at all)... and then we seem to have returned to those same earlier assumptions about relativity being wrong, but now you are armed with having purposely done some of the recipe while making sure to sabotage it so that you can say see, I tried and it didn't work.

I'd only introduce these extra dimensions to describe relationships which cannot be described with three variables. The torus you describe doesn't need more than 3, (before relativity). It doesn't need to be twisted up and embedded in R^4 as the 3 dimensional surface of a 4 dimensional donut.

I asked a simple question about T^2 (the standard, run of the mill torus) and you have jumped to this?

You said that you thought that it was okay to look at a sphere embedded in Euclidean 3-space so that you could use the Euclidean metric rather than an intrinsic one for the sphere... How do you do that? That takes us back to classical differential geometry and aspects of the first and second fundamental forms. For surfaces in Euclidean 3-space we are talking about some really messy math.

The nice property of the scwarzchild solution is that it is a steady solution, that is time independent. But admittedly, my higher dimensional description doesn't immediately give the necessary mechanics for considering motion/trajectories. But for relatively stationary observers, (relative to the star too), this method does accurately describe the spatial-temporal phenomenon they'd experience.

How can you be sure?

Lets go back to the cooking analogy... you say you want to have a taste of relativity, but while making this dish, you substitute two teaspoons of salt for two teaspoons of sugar, and where it asked for milk and eggs you used water. Afterwards you report that you had a taste of relativity but it just didn't work for you.

How can gravity be time independent if we are talking about accelerated frames... what observer in this setup would be stationary? Stationary relative to what? You want to look on this stuff with universal time... but the first thing you should know is that there is no such beast in relativity.

You talk about adding dimensions, but you threw out the most important one in favor the concept that leads just about everyone to paradoxes when thinking about relativity. And in the case of general relativity, the first step in looking at this should be to convert time from seconds to meters and look at it as a physical dimension. And this dimension is no more a throw-away dimension in the Schwarzschild Solution than the radial element was. You put all of your energy into one and totally ignored the other, and now think you've seen some real relativity.

No, you haven't. Relativity without the time aspect is not relativity at all.

Tell us, are you stationary right now? If you are sitting (and not falling), is that what you classify as stationary? What aspect of the Schwarzschild Solution (using universal time rather than the one in the metric) is keeping you on the face of the earth. If this is really time independent, then this should work out just fine, right?

The evidence is right before you The fact that three variables are not sufficient to describe relativistic space. Like I said before, it is really just a question of where you want your additional free variables to be -- as extra dimensions or as the coefficients in a non-constant metric. Take your pick. I like dimensions.

Space-time... and it works great if you don't cut corners... or dimensions.

The point I tried to make in my last post is that our familiar concept of space as a measurable expanse, is only a human construct, probably influence largely by the mechanics of vision. If you think of space algebraically, solely in terms of how many variables needed to describe the relationships between particles, it breaks down the traditional notion of space, and you don't see any Russian dolls.

Which is fine for ideas based on gauge theories... but I get the strong feeling that if you are this resistant to metrics on curved manifolds, connections on fiber bundles are going to rub you in the same wrong way.

But do you know what you are saying when you said "If you think of space algebraically"?

Algebraically in the case of the standard model is aspects of group theory. And not just any groups, Lie Groups. I've already described (in the terms I thought would translate best for the layperson) what groups are in this post above. But you need to know more than just groups, you should also understand how fiber bundles work... starting off with the tangent bundle, which is taught in most Riemannian Geometry courses.

I geared my math education towards this stuff knowing what I would be interested in. And I've seen the math that I had taken four full year series in turned into a semester course in many physics departments. At my school, both a course in modern abstract algebra and differentiable manifolds was required before taking the course on Lie Groups and Lie Algebras.

But none of that type of stuff from the standard model has worked in creating a particle theory of gravity.

Well the brane theory isn't my invention...

But what I say about gravitons must have some truth -- unlike other particles they must be able to escape black holes else black holes would have no external gravity. And since gravity is just a warping of space-time, gravitons must leave space-time through another dimension. A metric would not work here.

Additionally, this extra-dimensional ability of gravitons is the general belief why gravity is an exceptionally weak force.

Well, I haven't kept up my subscription to the theory of the month club, but the last time I read anything about gravitons, they were a replacement force particle for gravity... not something that existed side-by-side with space-time warping.

I've never heard of gravitons acting on gravitons to the point where they stopped doing what they were supposed to do (produce the effects of gravity), and gravitons are characters on a locally flat Minkowski spacetime. So a graviton theory wouldn't (to my understanding) have space-time warping and gravity particles together.

 

[Gepard]

 

[All Seeing Eye]

The Universe is expanding inside a cardboard box.

No seriously, the way I see it is the universe is infinite in size, the only thing expanding is the galaxies/stars/matter within the universe, I believe when you reach the edge of the physical universe its either just an infinity of nothingness/darkness or there's a large distance of nothingness/darkness and then you reach the edge of another area where there is expanding galaxies/stars/matter.

I think of it like this, you look into space and you see Galaxies and between those galaxies is huge voids of nothingness, well imagine those galaxies are infact universes and the voids between them are much much larger, so much larger that you can't see the other universes because they're so far apart.

As for the universe expanding, I believe eventually the expansion will begin to slow down and eventually stop and everything will simply remain at the same distances apart and no longer move apart from eachother.
Thats my view.