it was a response to your comments about 3d.....read through thread
Well, it was hard to tell... I was commenting about mathematics (specifically, differential topology). Were you commenting on mathematics? Do you even know what it was that I was doing in those drawings?
There are a number of programs (like Mathematica for example) which can display the
type of surface I was drawing (the Real Projective Plane), but all you'd be doing is looking at a predetermined surface.
One such application that does a nice job is 3D-XplorMath, which produced this animation of an immersion of the Real Projective Plane...
That nicely symmetric surface is a variation by Bryant & Kusner, and in that 3D application you can rotate and look at the surface from almost any view one can think of. But the Real Projective Plane isn't any one version of the immersion, because as a topological surface, it can be infinitely deformed.
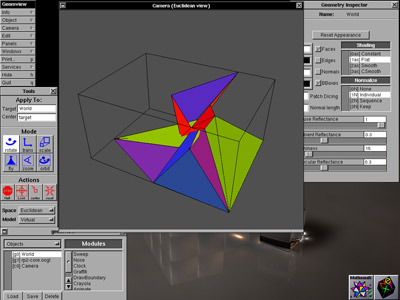
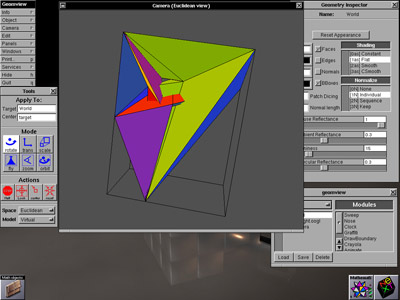
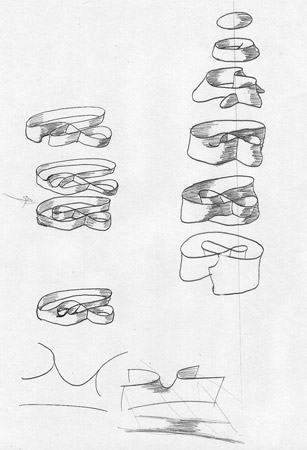
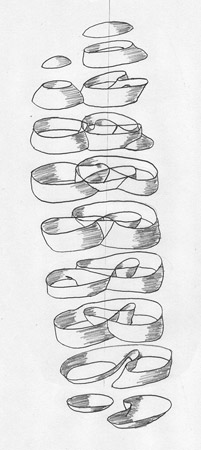
As a mental exercise I sit down with a pencil (and eraser) and a stack of paper (with absolutely no references), and start drawing a totally unique version of the Real Projective Plane. The last three images I posted in my first post are all the Real Projective Plane, they are equivalent under regular homotopy, and yet they are different from one another (because they were drawn at different times).
Do you do this type of mathematics? Do you model topological surfaces (starting with zero references)?
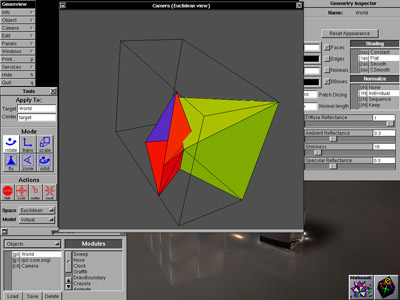
Don't get me wrong, I use 3D applications for mathematics. For example, this is a polyhedral version of the Real Projective Plane in a mathematics application (GeomView) that was developed at the
Geometry Center while I was there...
Again... is this the type of stuff that you do? Was this even what you were talking about? Because that is why I wasn't sure you were directing your comments towards me if this isn't what you had in mind.
I mean, I've done a (small) amount of 3D modeling... I had built a model of the USS Constellation over the course of three months back in the spring of 2007. I would say the results were mixed, but I was using antiques (1994 software on 1997 hardware).
And I'm not even remotely saying that that even comes close to truly having 3D modeling experience... because I only did it for about three months. And I surely wasn't commenting about that type of 3D work, as can be seen by looking at what I actually said (which you didn't quote)...
"I would consider the type of mathematics I do (differential topology) to be more like art, and I do all of it by hand. Because of the amount of visualization involved, I find computers to be more of a handicap than an aid. When drawing surfaces out by hand, you have to know what the surface is doing. It is the difference between active learning and passive learning."
BTW,
Shaw - I really like those topology drawings - they bring to mind works like those of M.C. Escher ("Escher-time!"

),
Thanks! Escher is one of my biggest inspirations.






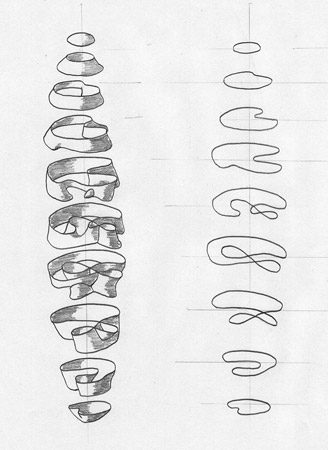
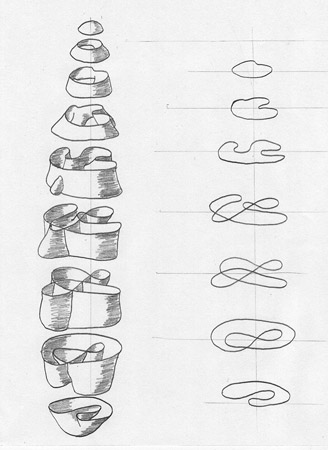

 )
)