The following video from Anton Petrov should address some of your questions. As with all things quantum mechanical, one cannot apply intuition derived from the behaviour of macroscale objects."Negative time" doesn't seem to accurately represent the described phenomenon. If one could measure changes in the energy state of the photon and the photon appeared to return to a previous state as it passed through matter, counter to some new state it takes on shortly after exiting the matter, then maybe negative time might apply.
The suggestion here is that energy is sometimes lost when matter has light travel through it. That makes sense in a probabilistic quantum universe, but in the end the sum total of energy would be accounted for. Could there be an "attitude" with which a photon can pass by an excited atom and steal some of that excitement? Can we measure changes in the energy state of a photon separate from its travel energy? Might some photons have more or less energy than others, even though they all travel at the same speed? Maybe photons can carry information like a payload, dropping some off and picking more up as they travel. If the initial early photons took information or energy away from the atoms they passed on their way through the matter, like a mail train hooking a sack of letters off the station's mail post without slowing down. The photons would leave that matter with less energy than before they passed, but now there's an empty hook (so to speak) upon which to catch new mail from the next train. ?
-Will
-
Welcome! The TrekBBS is the number one place to chat about Star Trek with like-minded fans.
If you are not already a member then please register an account and join in the discussion!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
The Nature of the Universe, Time Travel and More...
- Thread starter Will The Serious
- Start date
Something I have always wondered is where our solar system is located.
How different would the night sky look if our solar system was in a more densely packed part of the Galaxy?
I'm just also wondering if we were in a different location would that have effects on our climate, length of days, and seasons?
How different would the night sky look if our solar system was in a more densely packed part of the Galaxy?
I'm just also wondering if we were in a different location would that have effects on our climate, length of days, and seasons?
It seems unlikely, the sum total of gravitational influences from surrounding bodies would probably balance out to the same, but if your question is open to all possible conditions, it seems likely our Sun would be a different kinds of star. That would certainly have an effect. We may also have more comets and asteroids to deal with. Another significant factor in weather conditions.
-Will
-Will
The night sky would also be more interesting. There would be an increased numbers of high eccentricity long-period comets in the inner solar system due to perturbation of the Oort Cloud, increased probability of planetary bombardment by such comets, and potential disruption of planetary orbits by nearby passing stars would be more likely.Something I have always wondered is where our solar system is located.
How different would the night sky look if our solar system was in a more densely packed part of the Galaxy?
I'm just also wondering if we were in a different location would that have effects on our climate, length of days, and seasons?
As for the current location of our solar system - expect planetary bombardment in only 1.29 million years time when Gilese 710 will pass the Sun at a distance of 10,730 AU (0.167 light years). However, the increase in the cratering rate is estimated to be only about 5%. That is the end of the weather forecast...
Gliese 710 - Wikipedia
It seems unlikely, the sum total of gravitational influences from surrounding bodies would probably balance out to the same, but if your question is open to all possible conditions, it seems likely our Sun would be a different kinds of star. That would certainly have an effect. We may also have more comets and asteroids to deal with. Another significant factor in weather conditions.
-Will
Well I meant our whole solar system including our sun..... What if it was in a more dense area of the galaxy? Same orbits, same sun, just it's in a different location.
The increased density of stars and other celestial matter, as Asbo points out, would increase the regional activity. For example, the Chicxulub impactor hit Earth 66 million years ago and was a major factor in the mass extinction of dinosaurs.
An asteroid of that size also likely knocked a big chunk of atmosphere and water off the planet and into space. It could even be that some of the ice comets that we see periodically revisiting our solar system are a direct result of such an impact. A massive ball of water is splashed off the planet and over a short period of time, it freezes as it looses radiant energy and forms a ball of ice from the moving cloud of water vapor and atmospheric gasses.
In a denser region of space, we may actually become devoid of an atmosphere to even have weather. Of course, maybe some other nearby solar system would stiffer the same fate as Earth and the resultant ice comet could crash into us, not only replenishing our water and atmosphere, but bringing with it the seeds of whatever life may have been carried away within that ball of frozen material.
-Will
An asteroid of that size also likely knocked a big chunk of atmosphere and water off the planet and into space. It could even be that some of the ice comets that we see periodically revisiting our solar system are a direct result of such an impact. A massive ball of water is splashed off the planet and over a short period of time, it freezes as it looses radiant energy and forms a ball of ice from the moving cloud of water vapor and atmospheric gasses.
In a denser region of space, we may actually become devoid of an atmosphere to even have weather. Of course, maybe some other nearby solar system would stiffer the same fate as Earth and the resultant ice comet could crash into us, not only replenishing our water and atmosphere, but bringing with it the seeds of whatever life may have been carried away within that ball of frozen material.
-Will
Last edited:
Comets carrying the seeds of life may well have been what created life on our world ?
Forming on our world or seeded from somewhere else, the question of how life first formed is still the same. Presumably, if life can form anywhere in the universe, it formed under similar conditions as our own early cooling globe orbiting around the Sun. Given the nature of evolution and natural selection, where a seeded life came from, it would have had to be almost identical to the conditions it found here on Earth. So, the next question, if it could be shown to have come from an extraterrestrial origin, is, where is that?Comets carrying the seeds of life may well have been what created life on our world ?
If life was seeded from another planet, it very likely arrived by asteroid or comet that was formed during a massively destructive event. Therefore, we may not find anything but an odd asteroid-belt in orbit around its star. No life currently to be found.
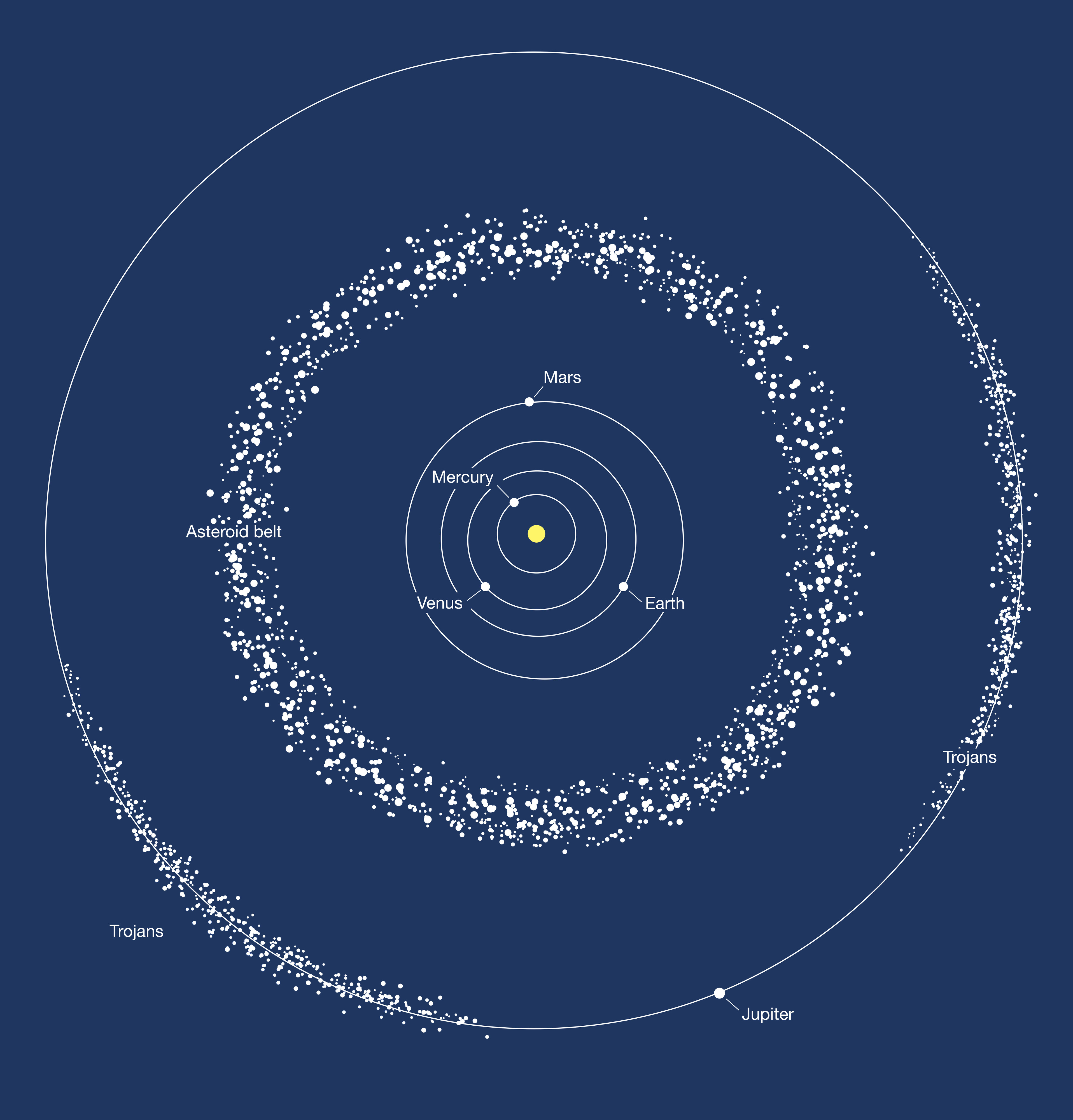
How much water is in our own asteroid belt, by the way?
-Will
The total mass of the asteroid belt is estimated to be about 3x10^21 kg, of which Ceres constitutes roughly one third. As Ceres is ~20% water by mass, that makes at least 2x10^20 kg of water in the belt. For comparison, the mass of all water on or near the surface of the Earth is estimated to be about nine times greater at 1.837x10^21 kg. This is only 0.031% of the Earth's mass, but there might be a lot more water locked up in the rocks of the interior - perhaps more than three times as much. The mass of water on Jupiter's moon Europa could be from two to three times greater than the amount on Earth's surface.
Last edited:
OK here's a quest
Maybe someone should convince Elon there's vast riches of diamonds in the belt...... They could be mined
The total mass of the asteroid belt is estimated to be about 3x10^21 kg, of which Ceres constitutes roughly one third. As Ceres is ~20% water by mass, that makes at least 2x10^20 kg of water in the belt. For comparison, the mass of all water on or near the surface of the Earth is estimated to be about nine times greater at 1.837x10^21 kg. This is only 0.031% of the Earth's mass, but there might be a lot more water locked up in the rocks of the interior - perhaps more than three times as much. The mass of water on Jupiter's moon Europa could be from two to three times greater than the amount on Earth's surface.
Maybe someone should convince Elon there's vast riches of diamonds in the belt...... They could be mined
He's from South Africa so I doubt diamonds impress him much. He's more into bitcoin. Also, if there is too much of a quantity, its value drops - scarcity has value.OK here's a quest
Maybe someone should convince Elon there's vast riches of diamonds in the belt...... They could be mined

This collapsed star is turning into an gigantic diamond before our eyes
Scientists have discovered a star that is in the process of crystallizing into a celestial diamond.
He's from South Africa so I doubt diamonds impress him much. He's more into bitcoin. Also, if there is too much of a quantity, its value drops - scarcity has value.

This collapsed star is turning into an gigantic diamond before our eyes
Scientists have discovered a star that is in the process of crystallizing into a celestial diamond.www.space.com
OK tell him the belt contains lots of something else he wants
Gullible rubes?OK tell him the belt contains lots of something else he wants
Last edited:
Mining them would be quite a problem. It'd be easier to make them ourselves. We already do that for some grades - they're only an allotrope of carbon after all. You'd think learning how to make and wrangle carbon nanotubes and graphene would be more appealing to a spacefaring technocrat. However, Musk seems to prefer stainless steel, so Fe rather than C. I guess he prefers brute force to finesse. I don't know why he's in such a hurry to get his ass to Mars.I think there may be sizable diamonds (relatively) nearby.
One of our two ice giants—also thought to have diamonds—looks to have been knocked over.
I can see diamonds knocked free out there.
Last edited:
Mining them would be quite a problem. It'd be easier to make them ourselves. We already do that for some grades - they're only an allotrope of carbon after all. You'd think learning how to make and wrangle carbon nanotubes and graphene would be more appealing to a spacefaring technocrat. However, Musk seems to prefer stainless steel, so Fe rather than C. I guess he prefers brute force to finesse. I don't know why he's in such a hurry to get his ass to Mars.
He clearly misses the family back home
OK tell him the belt contains lots of something else he wants
A legacy.I don't know why he's in such a hurry to get his ass to Mars.
I think one has been spotted by Hubble in the asteroid belt, and another was found on Mars. Very valuable, a lot of famous characters in history have spent their lives searching for one.
-Will
I don't know why he's in such a hurry to get his ass to Mars.
Maybe his urgency to go there was inspired by watching this scene from Total Recall.
Perhaps the scene played over and over like an endless loop in Musk's mind. Arnold could be quite persuasive.
To change the subject a little...
TIME
What is it? Can we effect it? If so, to what degree? Can we move ourselves or other objects (particles) back and forth through it? Can we jump across it? Can we buy time?
This article suggests that time is an emergent value rather than an absolute.
Several studies claim that "time is an illusion" and doesn't exist as we know it: By Eric Ralls Earth.com staff writer
But Relativity?
Then the article mentions the role time plays in the second law of Thermodynamics.
But, what would time look like if it was universal and existed in its own independent state, then you removed matter? Where would Δ be in the formula ΔS=ΔQ/T?
If one were to believe in time travel, would the flow of time, "universal" time, be reversible everywhere, or only locally? If it was reversible, then all the universe would flow backwards, just for the sake of the time traveler. It would, it seems, take an enormous amount of energy to reverse the universe or even a large enough localized time of any useful size.
Maybe Not reversed, but jumped across a fold in space-time? But that would require the parallel existence of all moments in the past with the present, and I would assume, the future too. Such a state would automatically reduce time to an emergent value because time could only exists within the timeline, and the timeline is static with only our awareness changing position along it.
One more thing, the article said,
-Will
TIME
What is it? Can we effect it? If so, to what degree? Can we move ourselves or other objects (particles) back and forth through it? Can we jump across it? Can we buy time?

This article suggests that time is an emergent value rather than an absolute.
Several studies claim that "time is an illusion" and doesn't exist as we know it: By Eric Ralls Earth.com staff writer
Some researchers claim that time may not exist in any fundamental way. They argue that our deeply held belief in a flowing “now” might be a trick of perception.
But Relativity?
Researchers have shown that gravity can slow clocks. So, for instance, time passes a little bit slower at sea level compared to the top of a mountain, because you’re a bit closer to Earth’s gravity.
It’s relative, meaning that time can move differently depending on how fast you’re moving or how close you are to a strong gravitational field
Then the article mentions the role time plays in the second law of Thermodynamics.
From the article:The second law states that there exists a useful state variable called entropy. The change in entropy (delta S, ΔS) is equal to the heat transfer (delta Q, ΔQ) divided by the temperature (T).
ΔS=ΔQ/T
For a given physical process, the entropy of the system and the environment will remain a constant if the process can be reversed.
-NASA
According to the second law of thermodynamics, entropy in an isolated system always tends to increase over time. In simple terms, things naturally move from order to disorder.
But, what would time look like if it was universal and existed in its own independent state, then you removed matter? Where would Δ be in the formula ΔS=ΔQ/T?
If one were to believe in time travel, would the flow of time, "universal" time, be reversible everywhere, or only locally? If it was reversible, then all the universe would flow backwards, just for the sake of the time traveler. It would, it seems, take an enormous amount of energy to reverse the universe or even a large enough localized time of any useful size.
Maybe Not reversed, but jumped across a fold in space-time? But that would require the parallel existence of all moments in the past with the present, and I would assume, the future too. Such a state would automatically reduce time to an emergent value because time could only exists within the timeline, and the timeline is static with only our awareness changing position along it.
One more thing, the article said,
I feel we have more senses then the five normal ones and that controversial 6th sense. A sense of time is one of the other senses we should include on the list.Time feels so obvious that we rarely question its existence. Our clocks tick, we sense the hours passing
-Will
Last edited:
You're missing the slash (/) in ΔS=ΔQ/T.
There are other formulations for entropy due to, for example, von Neumann, Gibbs*, Shannon, Bekenstein and Hawking, and, most famously, Boltzmann, which is inscribed on his tombstone:
S = k.log W
where k is Boltzmann's constant and W is the number of microstates in a system. In statistical thermodynamics, one can interpret entropy as a measure of the lack of knowledge about a system's internal configuration. For small enough systems, I believe spontaneous entropy reduction, which looks like time reversal, has been observed, confirming that the second law is indeed probabilistic. However, the probability of Humpty Dumpty spontaneously reassembling and leaping back onto the wall is vanishingly small.
Boltzmann took his own life and some ascribe his preceding depression to not only undiagnosed bipolar disorder, but also realising that he could not eliminate circular reasoning when he tried to explain time in terms of entropy.
The arrow of time does not arise from equations - it's something we deduce - and our brains are driven by increasing entropy that appears to be correlated with the expansion of the universe. Its entropy is potentially limited by the area of the observable horizon, although some solutions of the Einstein field equations of General Relativity suggest there might exist even higher entropy regions within - J A Wheeler's so-called "bags of gold".
A few decades ago, I remember reading a suggestion that equations about entropy, such as its rate of development over time, remain to be formulated. However, I don't know if anything came of that.
A more current development is Wolfram's ruliad** approach, which he claims can explain entropy, time and a whole lot besides. I don't understand it well enough to discern whether it also falls into a circular logical fallacy.
ETA:
* Gibbs' definition of entropy can be applied to a system far from thermal equilibrium. Other equations for entropy assume that a system is in thermal equilibrium.
** The Concept of the Ruliad
There are other formulations for entropy due to, for example, von Neumann, Gibbs*, Shannon, Bekenstein and Hawking, and, most famously, Boltzmann, which is inscribed on his tombstone:
S = k.log W
where k is Boltzmann's constant and W is the number of microstates in a system. In statistical thermodynamics, one can interpret entropy as a measure of the lack of knowledge about a system's internal configuration. For small enough systems, I believe spontaneous entropy reduction, which looks like time reversal, has been observed, confirming that the second law is indeed probabilistic. However, the probability of Humpty Dumpty spontaneously reassembling and leaping back onto the wall is vanishingly small.
Boltzmann took his own life and some ascribe his preceding depression to not only undiagnosed bipolar disorder, but also realising that he could not eliminate circular reasoning when he tried to explain time in terms of entropy.
The arrow of time does not arise from equations - it's something we deduce - and our brains are driven by increasing entropy that appears to be correlated with the expansion of the universe. Its entropy is potentially limited by the area of the observable horizon, although some solutions of the Einstein field equations of General Relativity suggest there might exist even higher entropy regions within - J A Wheeler's so-called "bags of gold".
A few decades ago, I remember reading a suggestion that equations about entropy, such as its rate of development over time, remain to be formulated. However, I don't know if anything came of that.
A more current development is Wolfram's ruliad** approach, which he claims can explain entropy, time and a whole lot besides. I don't understand it well enough to discern whether it also falls into a circular logical fallacy.
ETA:
* Gibbs' definition of entropy can be applied to a system far from thermal equilibrium. Other equations for entropy assume that a system is in thermal equilibrium.
** The Concept of the Ruliad
Last edited:
Similar threads
- Replies
- 3
- Views
- 3K
Contest: ENTER
June 2025 Art Challenge - Suggest Your Themes!
- Replies
- 3
- Views
- 4K
If you are not already a member then please register an account and join in the discussion!
