If we were to stand outside of space-time then would we see that time does not flow but is rather a static pattern a la the beliefs of Gödel and Rudy Rucker? Would it have always been there? Is it eternal and just experienced by us like a record is experienced by a needle? (Whoops, did I just give away my age?) Anyway, what are your thoughts?
-
Welcome! The TrekBBS is the number one place to chat about Star Trek with like-minded fans.
If you are not already a member then please register an account and join in the discussion!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Outside Space-Time
- Thread starter Zameaze
- Start date
The biggest problem with how most people see time is that they don't seem to realize that time is a displacement measurement rather than a coordinate measurement.
Lets play a game... take a piece of paper and a pencil. Hold the pencil lead to the paper at a point in the middle and don't lift it from the page. Now move it to some other point on the page. That mark on the page, the arc length of it, is time.
Now attempt (while keeping the lead still on the page) to move a negative distance.
It is obvious that any movement will add to the arc length and that you can't make a move that shortens the curve you are drawing on the page. Time is like that.
What is funny is that all of space is like that as well. People like to apply coordinates to space, but they are essentially meaningless. You've never occupied the same point in space twice. You can't. You are constantly moving away from any previous point that you existed in (each of those points is known as an event).
So everything is actually a measure of arc length, and it is actually best to think of time in terms of distance (meters or feet) rather than seconds. So the reason you can't move backwards in time is the same reason you can't move a negative distance in space.
There are a ton of philosophical implications once you look at time as it is rather than how it is experienced... but that is the fun of this type of stuff.
Lets play a game... take a piece of paper and a pencil. Hold the pencil lead to the paper at a point in the middle and don't lift it from the page. Now move it to some other point on the page. That mark on the page, the arc length of it, is time.
Now attempt (while keeping the lead still on the page) to move a negative distance.
It is obvious that any movement will add to the arc length and that you can't make a move that shortens the curve you are drawing on the page. Time is like that.
What is funny is that all of space is like that as well. People like to apply coordinates to space, but they are essentially meaningless. You've never occupied the same point in space twice. You can't. You are constantly moving away from any previous point that you existed in (each of those points is known as an event).
So everything is actually a measure of arc length, and it is actually best to think of time in terms of distance (meters or feet) rather than seconds. So the reason you can't move backwards in time is the same reason you can't move a negative distance in space.
There are a ton of philosophical implications once you look at time as it is rather than how it is experienced... but that is the fun of this type of stuff.

From what I can tell (as an outsider looking in), there are a lot of physicists who seem to want to avoid the problems of time. But it has been that avoidance that has led directly to the failure of all quantum theories of gravity, and a weakening of quantum based theories dealing with large scales.
It is interesting how special relativity is embraced by particle theorists, but not general relativity. The thing that makes special relativity special is that it describes a situation that really doesn't occur in nature (non-accelerating reference frames). And while special relativity is interesting, describing special (very rare) cases makes for a limited area of application. General relativity looks at both non-accelerating and accelerating reference frames (so special relativity is actually a subset of general relativity). And time is as important (if not more important) an aspect of general relativity's description of gravity as space is.
For those who attempt to replace gravity with a force, they have to conveniently ignore the true nature of gravity.
For example, time on the surface of the earth is passing slower than it is further away from the planet. Time moves faster when you are in an airplane at 35,000 feet than when you are standing on the ground. And actually while standing on the ground time is moving faster for your head than your feet. These differences are so small that only the larger ones really show up (the difference between time on earth verses the time way out in orbit), and yet quantum/particle physicist who deal with imperceptibly small things all the time would rather ignore that in favor of a universal time.
Another nice example is the effect on space. Lets say that we enclosed the earth in a large sphere who's surface area is X. If we lived in euclidean flat space, then we would expect that knowing X we would also know the enclosed volume Y. After all Volume is given by 4/3πr^3 and surface area by 4πr^2. So if X=4πr^2, and we derive Y'=4/3πr^3, what we actually find is that the real volume (Y) of that sphere enclosing the earth is greater than that of Y'. And that is because the r in X=4πr^2 isn't the real distance to the center of the sphere, that real distance is larger.
These concepts become important in the study of general relativity because if you use a polar coordinate system, the r that you use is based on the r from the spherical area, and not the actual distance to the center where you've placed the mass-energy (which is effected by that mass-energy).
These aspects of nature aren't explained in any version of quantum gravity to date. And their failings (in my opinion) is based on attempts to make gravity a force, when in all actuality the force is a byproduct of what is happening.
At quantum scales (remembering that all of quantum physics is probabilities) time seems fuzzy, and not everything seems to follow causal paths. So a lot of things like tachyons pop up when making attempts to translate quantum physics to larger scales.
But even then, those are also interesting aspects of the nature of time. On large scales, even those there isn't a universal time, you can work out a causal path (world lines) of everything... but at quantum scales causal paths seemingly break down (or at least our ability to truly see what is happening does).
Sorry for the long post.
It is interesting how special relativity is embraced by particle theorists, but not general relativity. The thing that makes special relativity special is that it describes a situation that really doesn't occur in nature (non-accelerating reference frames). And while special relativity is interesting, describing special (very rare) cases makes for a limited area of application. General relativity looks at both non-accelerating and accelerating reference frames (so special relativity is actually a subset of general relativity). And time is as important (if not more important) an aspect of general relativity's description of gravity as space is.
For those who attempt to replace gravity with a force, they have to conveniently ignore the true nature of gravity.
For example, time on the surface of the earth is passing slower than it is further away from the planet. Time moves faster when you are in an airplane at 35,000 feet than when you are standing on the ground. And actually while standing on the ground time is moving faster for your head than your feet. These differences are so small that only the larger ones really show up (the difference between time on earth verses the time way out in orbit), and yet quantum/particle physicist who deal with imperceptibly small things all the time would rather ignore that in favor of a universal time.
Another nice example is the effect on space. Lets say that we enclosed the earth in a large sphere who's surface area is X. If we lived in euclidean flat space, then we would expect that knowing X we would also know the enclosed volume Y. After all Volume is given by 4/3πr^3 and surface area by 4πr^2. So if X=4πr^2, and we derive Y'=4/3πr^3, what we actually find is that the real volume (Y) of that sphere enclosing the earth is greater than that of Y'. And that is because the r in X=4πr^2 isn't the real distance to the center of the sphere, that real distance is larger.
These concepts become important in the study of general relativity because if you use a polar coordinate system, the r that you use is based on the r from the spherical area, and not the actual distance to the center where you've placed the mass-energy (which is effected by that mass-energy).
These aspects of nature aren't explained in any version of quantum gravity to date. And their failings (in my opinion) is based on attempts to make gravity a force, when in all actuality the force is a byproduct of what is happening.
At quantum scales (remembering that all of quantum physics is probabilities) time seems fuzzy, and not everything seems to follow causal paths. So a lot of things like tachyons pop up when making attempts to translate quantum physics to larger scales.
But even then, those are also interesting aspects of the nature of time. On large scales, even those there isn't a universal time, you can work out a causal path (world lines) of everything... but at quantum scales causal paths seemingly break down (or at least our ability to truly see what is happening does).
Sorry for the long post.

ProtoAvatar
Fleet Captain
[...]
Another nice example is the effect on space. Lets say that we enclosed the earth in a large sphere who's surface area is X. If we lived in euclidean flat space, then we would expect that knowing X we would also know the enclosed volume Y. After all Volume is given by 4/3πr^3 and surface area by 4πr^2. So if X=4πr^2, and we derive Y'=4/3πr^3, what we actually find is that the real volume (Y) of that sphere enclosing the earth is greater than that of Y'. And that is because the r in X=4πr^2 isn't the real distance to the center of the sphere, that real distance is larger.
[...]
How can this 'real distance' be measured, practically?
By using light, sending a ray of light to the other side of the shpere and noting how much time passed until the ray of light returns?
Well, there is the obvious problem of having the earth in the way, but there is another way to measure that effect... two concentric spheres about the earth, one quite a bit larger than the other (the smaller one could be near the surface of the earth if you wanted). The effect would be noticeable in the difference in distances between the two surfaces compared to how they would have been in euclidean space based on their surface areas.How can this 'real distance' be measured, practically?
By using light, sending a ray of light to the other side of the shpere and noting how much time passed until the ray of light returns?
So yes it can be practically measured, and has (as has the time dilation for near paths like those of airplanes). The first measurable test was Mercury's orbit, but better measurements have been done since then.
Slightly off topic... people wonder what it would seem like to fall into a black hole. One of the things that one might notice is that the black hole seems further away as you get closer. In the two dimensional representation it is shown as a funnel, but what it would seem like is one of those dreams where as you run down a hallway the end gets further and further away from you.
Of course time stops when you hit the event horizon. But by that point your mass has actually moved the real event horizon out further beyond you. What you should end up with is onion layers of frozen time as the event horizon slowly grew out from the center of the original star (spinning black holes are different in that you have additional energy to take into account).
....Of course time stops when you hit the event horizon....
OK, I'm not following (which is not terribly unusual for me). If time is a displacement measurement, how can time stop?
BTW, have you read any of John W. Moffat's work? If so, what do you think of his nonsingular solution of Einstein's field equations in general relativity? His solution does not possess a black hole event horizon.
As a displacement, you can have zero or positive values for time, just not negative ones. Hitting an event horizon in the pencil and paper analogy is hitting the edge of the page. Time also stops if you don't move the pencil lead from a point.....Of course time stops when you hit the event horizon....
OK, I'm not following (which is not terribly unusual for me). If time is a displacement measurement, how can time stop?
I haven't, but as I recall he is one of the people who was talking about variable speeds for the speed of light.BTW, have you read any of John W. Moffat's work?
When one thinks about it, the speed of light is our only means of measuring the universe... our only ruler. The speed of light could be changing and we wouldn't know it.
But there might be some type of effect on the universe around us. For example, if the speed of light were slowing, then the universe might seem like it is expanding even if it were actually static. If there was a significant change (a dramatic slowing) we might observe a hyper expansion of the universe. And because in every way we can tell the speed of light is a constant (and our own reference frames distort to keep it so), we wouldn't ever suspect that it was changing in anyway.

That type of stuff is fun to contemplate... and I'd love to spend more time doing so.

ProtoAvatar
Fleet Captain
Well, there is the obvious problem of having the earth in the way, but there is another way to measure that effect... two concentric spheres about the earth, one quite a bit larger than the other (the smaller one could be near the surface of the earth if you wanted). The effect would be noticeable in the difference in distances between the two surfaces compared to how they would have been in euclidean space based on their surface areas.How can this 'real distance' be measured, practically?
By using light, sending a ray of light to the other side of the shpere and noting how much time passed until the ray of light returns?
So yes it can be practically measured, and has (as has the time dilation for near paths like those of airplanes). The first measurable test was Mercury's orbit, but better measurements have been done since then.
The measurement of the 'real distance':
Does it measure the cumulative effects of both time dilation and space curvature, or is only the space curvature measured (time dilation being calculated and then mathematically removed from the empirical data in order to obtain this 'real distance')?
About black holes:Slightly off topic... people wonder what it would seem like to fall into a black hole. One of the things that one might notice is that the black hole seems further away as you get closer. In the two dimensional representation it is shown as a funnel, but what it would seem like is one of those dreams where as you run down a hallway the end gets further and further away from you.
Of course time stops when you hit the event horizon. But by that point your mass has actually moved the real event horizon out further beyond you. What you should end up with is onion layers of frozen time as the event horizon slowly grew out from the center of the original star (spinning black holes are different in that you have additional energy to take into account).
As I understand it, time only stands still in the singularity. At the event horizon, time is only ridiculously dilated (almost frozen, but not completely).
So - for an observer ouside the event horizon (POV A), the person falling in the blach hole (POV B) would 'almost' freeze at the event horizon (practically speaking, it would take an enourmos amount of time for POV B to reach the singularity). Ironically, the person falling in the black hole (meaning the person who's as good as dead) will almost certainly outlast the observer's civilization.
Interestingly, this means that from the observer's perspective (our perspective), nothing that fell into the black hole ever reached the actual singularity. In other words, the black hole is made up of the singularity (created in collapse of the innitial star) and a shell of matter found just beyond the event horizon.
However, from POV B, all these aeons will only take a few seconds - from his perspective, time flows normally, and it's the universe outside the event horizon that experiences a ridiculous fast forward.
Apropos spinning black holes:
Shaw, how do you reconcile your model of time that forbids travel back into the past with the general relativity solution that permits this kind of time travel by flying around a spinning singularity and, using its frame-dragging, surpassing the speed of light?
Last edited:
...But there might be some type of effect on the universe around us. For example, if the speed of light were slowing, then the universe might seem like it is expanding even if it were actually static. If there was a significant change (a dramatic slowing) we might observe a hyper expansion of the universe....
What a cool idea! It seems like we could get rid of dark matter and the pioneer anomaly in one fell swoop.
ProtoAvatar
Fleet Captain
...But there might be some type of effect on the universe around us. For example, if the speed of light were slowing, then the universe might seem like it is expanding even if it were actually static. If there was a significant change (a dramatic slowing) we might observe a hyper expansion of the universe....
What a cool idea! It seems like we could get rid of dark matter and the pioneer anomaly in one fell swoop.
No we can't.
Dark matter (a LOT of it) is needed to keep the galaxies together, not to generate the appearance that they're expanding.
And if we have dark matter, we need dark energy to overcome dark matter's gravity and to explain why the universe didn't already collapse in a big crunch.
Well, all real measurements are based on the speed of light, so both time and space effects should be looked at together, not separately. People want time and space to be separate, nature considers them to be pretty much the same thing. In fact, getting rid of "seconds" as a unit of measurement of time and replacing it with "meters" makes working with this stuff a lot easier. So replace 1 second with 3x10^8 meters, then consider the measurements.The measurement of the 'real distance':
Does it measure the cumulative effects of both time dilation and space curvature, or is only the space curvature measured (time dilation being calculated and then mathematically removed from the empirical data in order to obtain this 'real distance')?
All of this stuff revolves around arc length (ds) of world paths. And when figuring that out you need to apply the metric of the space (manifold). Minkowski space has a non-Riemannian metric, general relativity just modified the metric to be a function of mass-energy, but it is still a measure of arc length. The metric in Minkowski space is...
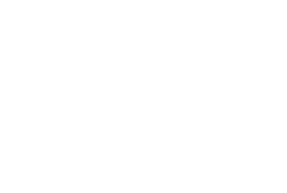
while the metric (in polar coordinates and generalized) of the space-time manifold of general relativity is...
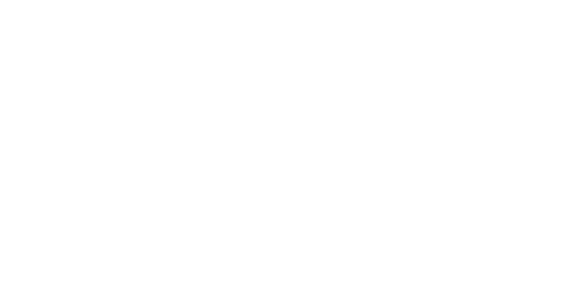
All real measurements have to be based on the speed of light because that is the only measuring rod that is independent of reference frame. So just as there is no real (universal) time, there is also no real (universal) measure of length, because both are subject to frame of reference.
The event horizon is the boundry of the singularity. The term singularity is defined as a point or region where a manifold becomes non-differentiable. Beyond the event horizon is the singularity... there isn't additional space between the event horizon and the singularity.About black holes:
As I understand it, time only stands still in the singularity. At the event horizon, time is only ridiculously dilated (almost frozen, but not completely).
As for the effect on time, look at the equation above and note that the event horizon is defined as r=2M, which in turn forces the time component to zero.
And there is the truth of this... because black holes don't just pop into existence.Interestingly, this means that from the observer's perspective (our perspective), nothing that fell into the black hole ever reached the actual singularity. In other words, the black hole is made up of the singularity (created in collapse of the innitial star) and a shell of matter found just beyond the event horizon.
A black hole starts at the center of a massive star when enough of it's core collapse with a sphere who's radius is twice that mass (the radius being determined by surface area of the sphere, not the diameter to the center). It could have been a pound of matter, it could have been millions of tons, but it started relatively small compared to the overall size of the star.
Well, you have an event horizon inside of a star, with matter collapsing down on it, unit time stops for that matter... but that shell of matter has moved the real event horizon further out. Repeat this until the star is gone behind an event horizon and now you have a black hole.
The thing to remember is that the new layers can't have any effect on the previous ones. Partially because the previous ones are frozen in time, and also because a uniform spherical shell produces no gravitational effect on it's interior.
As a black hole grows (it's event horizon gets bigger) those previous shells are unaware of any effect... including the fact that their very presence (as mass-energy) caused the event horizon they were falling towards to extend out behind them.
Well, first of all, I don't get to take credit (or blame) for that model of time.Apropos spinning black holes:
Shaw, how do you reconcile your model of time that forbids travel back into the past with the general relativity solution that permits this kind of time travel by flying around a spinning singularity and, using its frame-dragging, surpassing the speed of light?
Second, I never got as far as spinning black holes. By the time I had gotten to the point where I could have studied them my interests had been pulled towards research in differential topology and homotopy theory. My passion for physics was largely based on wanting to understand what gravity was, and once I had reached a level of understanding I was happy with I turned towards pure mathematics.
So in the area of spinning black holes I profess ignorance of the mechanisms at play.

Remember that that was a thought experiment. In that experiment the condition was that the universe was fixed and the speed of light was changing. Just like the big bang could have been a drastic reduction in the speed of light, the big crunch could be a drastic increase in the speed of light. All other things being equal, light would not be effected by gravity as light would still be independent of reference frame.No we can't.
Dark matter (a LOT of it) is needed to keep the galaxies together, not to generate the appearance that they're expanding.
And if we have dark matter, we need dark energy to overcome dark matter's gravity and to explain why the universe didn't already collapse in a big crunch.
But again... it was a thought experiment based on someone's overly simplified notion of the speed of light changing. I don't actually know anything about their theories or how they work, but even without that it made for an interesting mental exercise (and little more).
I hate dark matter and dark energy. If we need dark matter to keep us from flying apart and then have to posit dark energy to keep us from doing the opposite, it would seem that there is something fundamentally wrong with the theory. Also, if E=mc^2 is correct then doesn’t that point to dark energy and dark matter being the same thing.
And while we are on it, it doesn’t seem plausible that for each and every galaxy dark matter always collects around visible matter in the same fixed ratio. I mean it’s not impossible, but it doesn’t seem likely. OK, I’m going to quit now--my head hurts.
And while we are on it, it doesn’t seem plausible that for each and every galaxy dark matter always collects around visible matter in the same fixed ratio. I mean it’s not impossible, but it doesn’t seem likely. OK, I’m going to quit now--my head hurts.
ProtoAvatar
Fleet Captain
Well, all real measurements are based on the speed of light, so both time and space effects should be looked at together, not separately. People want time and space to be separate, nature considers them to be pretty much the same thing. In fact, getting rid of "seconds" as a unit of measurement of time and replacing it with "meters" makes working with this stuff a lot easier. So replace 1 second with 3x10^8 meters, then consider the measurements.The measurement of the 'real distance':
Does it measure the cumulative effects of both time dilation and space curvature, or is only the space curvature measured (time dilation being calculated and then mathematically removed from the empirical data in order to obtain this 'real distance')?
All of this stuff revolves around arc length (ds) of world paths.
By "arc lenghts of world paths" you refer to the trajectory of a photon - or another phisical object in a gravitational field, yes?
I understand what you say about treating time dilation and space curvature, essentially, only as space curvature.
I'm sure it makes the calculations easier.
But, as far as understanding the effects of mass goes, it seems to simplify the picture. Consider:
In euclidean geometry, time/space is absolute.
Py picturing time dilation and space curvature ONLY as space curvature, one is essentially assuming the observer's time is absolute and mass only influences distance. BUT we know gravity influences BOTH space and time.
So - you can only calculate ds if you know the other 4 terms of the equation. They should be hard to measure - unless one can calculate dx, dy and dz if one knows the mass and position of the interacting objects.And when figuring that out you need to apply the metric of the space (manifold). Minkowski space has a non-Riemannian metric, general relativity just modified the metric to be a function of mass-energy, but it is still a measure of arc length. The metric in Minkowski space is...
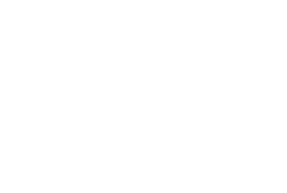
But, when an object reaches the event horizon, it doesn't turn into a shell. It adds matter only in a part of the singularity, but increases the radius of the event horizon around the entire singularity - I am assuming that the event horizon always has the shape of a sphere or an oval and not an irregular shape. And, because the object is frozen in time, it doesn't deform further. Thus, the singularity isn't an uniform sphere of matter - there are holes in it, empty spaces.The event horizon is the boundry of the singularity. The term singularity is defined as a point or region where a manifold becomes non-differentiable. Beyond the event horizon is the singularity... there isn't additional space between the event horizon and the singularity.About black holes:
As I understand it, time only stands still in the singularity. At the event horizon, time is only ridiculously dilated (almost frozen, but not completely).
As for the effect on time, look at the equation above and note that the event horizon is defined as r=2M, which in turn forces the time component to zero.
And there is the truth of this... because black holes don't just pop into existence.
A black hole starts at the center of a massive star when enough of it's core collapse with a sphere who's radius is twice that mass (the radius being determined by surface area of the sphere, not the diameter to the center). It could have been a pound of matter, it could have been millions of tons, but it started relatively small compared to the overall size of the star.
Well, you have an event horizon inside of a star, with matter collapsing down on it, unit time stops for that matter... but that shell of matter has moved the real event horizon further out. Repeat this until the star is gone behind an event horizon and now you have a black hole.
The thing to remember is that the new layers can't have any effect on the previous ones. Partially because the previous ones are frozen in time, and also because a uniform spherical shell produces no gravitational effect on it's interior.
As a black hole grows (it's event horizon gets bigger) those previous shells are unaware of any effect... including the fact that their very presence (as mass-energy) caused the event horizon they were falling towards to extend out behind them.
Also - I often heard that a singularity has an infinitely small volume and is infinitely dense. How can this be reconciled with this model for a black hole? Is this referring only to the initial singularity and not to the matter that subsequently fell into the black hole?
Apropos spinning objects:Well, first of all, I don't get to take credit (or blame) for that model of time.Apropos spinning black holes:
Shaw, how do you reconcile your model of time that forbids travel back into the past with the general relativity solution that permits this kind of time travel by flying around a spinning singularity and, using its frame-dragging, surpassing the speed of light?
Second, I never got as far as spinning black holes. By the time I had gotten to the point where I could have studied them my interests had been pulled towards research in differential topology and homotopy theory. My passion for physics was largely based on wanting to understand what gravity was, and once I had reached a level of understanding I was happy with I turned towards pure mathematics.
So in the area of spinning black holes I profess ignorance of the mechanisms at play.
The Sagnac Effect seems to imply strongly that, in non-inertial frames, simultaneity is NOT relative.
Last edited:
I remember and article in Scientific American about twenty years ago that said you COULD travel in time.
All you need is a massive object, like the Sun, and be moving towards it at close to the speed of light.
Like the method used in ST4.
But, there again I remember reading somewhere that Viking had found life, a type of moss, on Mars, but that didn't count!!
All you need is a massive object, like the Sun, and be moving towards it at close to the speed of light.
Like the method used in ST4.
But, there again I remember reading somewhere that Viking had found life, a type of moss, on Mars, but that didn't count!!
Would you tell us Shaw, how we take the metric you've described, and calculate a satellite's trajectory with it? You've talked about geodesics before, and I do remember (more or less) what those are, but only in spatial manifolds. I'm unsure how we express things like the velocity of a satellite, where we're dealing with a space-time manifold.
World paths are there if you are moving or not. Stand on the surface of a planetary body that is not rotating and is in the middle of an empty universe... you need not have any spatial displacement, yet there is a displacement, and you feel the effect on that displacement as gravity. The actual effect on the displacement is on the time component, which is what is creating the accelerated reference frame.By "arc lenghts of world paths" you refer to the trajectory of a photon - or another phisical object in a gravitational field, yes?
Well, you have to remember that while we are treating the units as the same thing, the signature of the metric is absolutely non-euclidean (non-Riemannian) in nature. Even a flat manifold with a metric like that is not going to act like euclidean space.I understand what you say about treating time dilation and space curvature, essentially, only as space curvature.
I'm sure it makes the calculations easier.
But, as far as understanding the effects of mass goes, it seems to simplify the picture. Consider:
In euclidean geometry, time/space is absolute.
Py picturing time dilation and space curvature ONLY as space curvature, one is essentially assuming the observer's time is absolute and mass only influences distance. BUT we know gravity influences BOTH space and time.
More importantly, separating time is the biggest problem I see with anyone attempting this stuff. If you want to simplify, remove one (or two) of the spatial components. Remember that gravity is an accelerated reference frame, that requires time to be in play. The spatial aspects point you in the right direction, but curved space isn't gravity without the time aspect.
When you try to solve the equations of relativity without time, there is no accelerated reference frame, which is what we see as a force, so a test particle at rest (floating in mid air) would stay at rest in such a situation. If it was moving, it might follow a curved path based on the curvature of space, but what makes the earth press upwards against your feet is cause by time.
Universal time negates gravity (in general relativity).
That part isn't that hard... you can learn it in a standard classical differential geometry course. The key is that dx, dy and dz can be based on what ever coordinate system you want. Better yet, ignoring them altogether and working with this stuff in a coordinate free way will yield better information about the global geometry.So - you can only calculate ds if you know the other 4 terms of the equation. They should be hard to measure - unless one can calculate dx, dy and dz if one knows the mass and position of the interacting objects.
For example (short, as it is getting off topic), let say you have a curve on the surface of a 2-manifold like a sphere. The curve is parameterized by arc length, and you want to know something about it relative to the surface. It is a 2 dimensional surface, so you pick some easy coordinates for the surface at the start of the curve... but maybe those coordinates aren't as nice the further along you go, so you pick some others. And all the while, the surface doesn't care how you are parameterizing it.
And that is important when you start to deal with space-time of general relativity as the surface isn't regular (does have a nice fixed metric on the manifold), instead it has a metric that is effected by mass-energy.
Well, are we talking about the growing of the black hole from within a star or the effect of a small object as if falls towards a fully formed black hole?But, when an object reaches the event horizon, it doesn't turn into a shell. It adds matter only in a part of the singularity, but increases the radius of the event horizon around the entire singularity. And, because the object is frozen in time, it doesn't deform further.
Thus, the singularity isn't an uniform sphere of matter - there are holes in it, empty spaces.
You are right... it isn't uniform, but what extent of effect are you worried about. It is less than the effect that you have on the earth by jumping up and down. It effects things, but not so much that you're talking about anything we would discuss here.
Now if you want to talk about another star or black hole falling straight into a non-spinning black hole, then sure, the geometry will be significantly altered... but that is beyond what we are discussing.
Frankly, until someone has a really good grasp of the simplest model, there is no point in attempting to discuss the more complex ones. And the more complex ones are really complex (and I didn't get that far along in this stuff).
Don't believe everything that you hear?Also - I often heard that a singularity has an infinitely small volume. How can this be reconciled with this model for a black hole?
The example I gave earlier in the thread about a spherical shell about the earth having a larger volume than the surface area would normally have enclosed if it was empty (or in euclidean space) works just as well here. When taken to the extremes of a black hole, the distance to the center of a spherical shell about one could be greater than the distance around the circumference of the sphere.
The reason for learning differential geometry slowly, starting out with classical differential geometry of surfaces, learning about the first and second fundamental forms, is really to build up an intuition about how this stuff works before you discard many of those tools for newer ones that are more powerful and work in more exotic situations. Sadly most physicist learn their differential geometry at the same time they are learning relativity.
I mean you already have a better grasp of this stuff than some people with degrees in physics based on our conversation so far. But far too many physics students will never see any of this stuff.

The important aspect of finding a geodesic on any manifold is applying the metric to find the covariant derivative (which for a geodesic path has to equal zero).Would you tell us Shaw, how we take the metric you've described, and calculate a satellite's trajectory with it? You've talked about geodesics before, and I do remember (more or less) what those are, but only in spatial manifolds. I'm unsure how we express things like the velocity of a satellite, where we're dealing with a space-time manifold.
So a satellite might have an initial momentum vector (which is a form of arc length parameterization which is both space and time dependent) and by knowing the covariant derivative (which is dependent on the metric, which in turn is dependent on the mass-energy of the planet, which is also effected by the distance from the planet) you can calculate the path. But the initial coordinate system might need changing too (unless you were starting with a satellite already in a stable orbit).
And it is the most messy process there is, which is why general relativity has not replaced Newtonian/Lagrangian mechanics for most applications.
Other than really simple examples, it wasn't until the wide availability of computers that people spent a lot of time applying general relativity to phenomena. It was just too painful to do by hand.

Honestly, just looking at my Riemannian Geometry book, I think it would take me a few days to get back to the point were I could set up the covariant derivative for some abstract manifold with a given metric... which I'd need to recall before being able to remember the steps for doing it in general relativity.
It is actually done with general relativity in The Geometry of Physics... but I can't seem to find my copy off hand.
I'm not sure if any of that was helpful to anyone... so I apologize for my shortcomings here.

Similar threads
- Replies
- 1
- Views
- 293
- Replies
- 9
- Views
- 848
- Replies
- 8
- Views
- 854
If you are not already a member then please register an account and join in the discussion!
