I would appreciate more depth on neural networks. I have written some simple ones in the past but getting straight information from an actual AI researcher would be great. 



That's really fascinating. It sounds a little bit similar to genetic programming, in which you have variations of an algorithm try to solve the same problem and then propagate and mutate whichever one(s) come closest, then do it over again.
That's really fascinating. It sounds a little bit similar to genetic programming, in which you have variations of an algorithm try to solve the same problem and then propagate and mutate whichever one(s) come closest, then do it over again.
I hadn't thought about it this way but I suppose on a cursory examination they do look similar.
However, Genetic Algorithms are modeled on "survival of the fittest" whereas Ensemble Learning is modeled on "wisdom of the crowds". They are actually two very different ideas.
Genetic algorithms are designed start with a large number of random "solutions", then whittle them down to a few or a single good solution. On the other hand, the goal of ensembles is to end up with a large number of diverse, partially-good classifiers. Without this diversity, ensemble learning can actually perform worse than many standard classifiers.

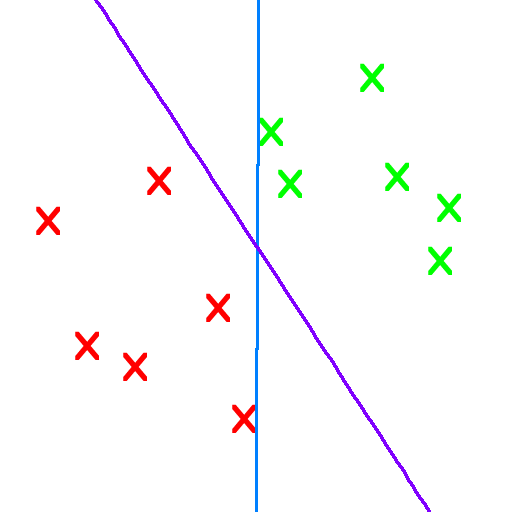
Purple. The blue line has two data points so close to the boundary that they touch it. That, and purple is always superior.
Yeah, I'm going with purple, because it seems to represent a "best fit" line between the two sets--it never draws too close to either.
There is not enough information to decide which is better. Reasonable criteria have been given for why the purple line is better. However, if the goal were to provide a boundary that is a function of x, the horizontal coordinate, then the blue line is a much better approximation of a vertical boundary. It depends by what one means by "better"; what is it exactly that you are trying to maximize?
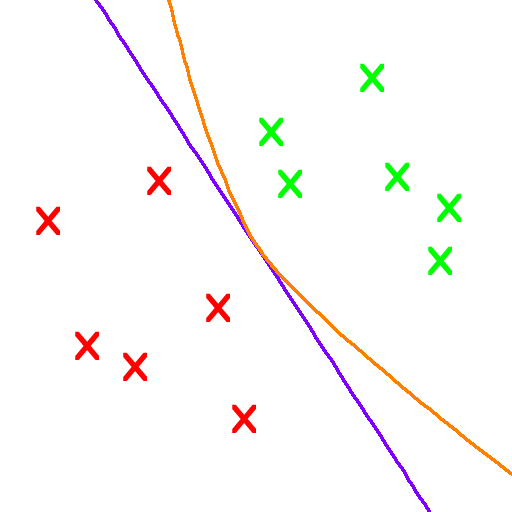
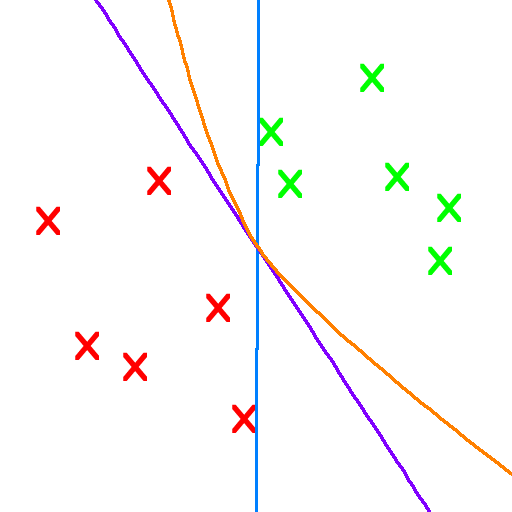


Many scientific fields have their own versions of the impossibility theorem. In Mathematics, there is Godel's Incompleteness Theorem which states roughly that any but the simplest toy mathematical system has facts that can never be proven or disproven. In Computer Science, Turing's Halting Theorem states that there are computer programs that will never stop running (In other words, are unable to solve certain tasks as they won't ever stop running or find a solution).
We use essential cookies to make this site work, and optional cookies to enhance your experience.