At least, I think it is. Bear with me. I kinda suck at math. It's my secret shame.
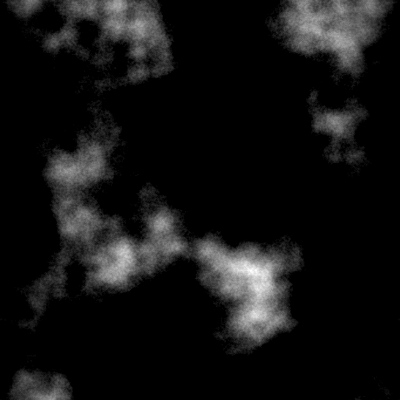
I have a program I'm working on that generates a heightmap using perlin noise. Straightforward stuff, right? For simplicity's sake, let's just say it creates an image of arbitrary size where each pixel has a value between 0 and 255, which is its height value.
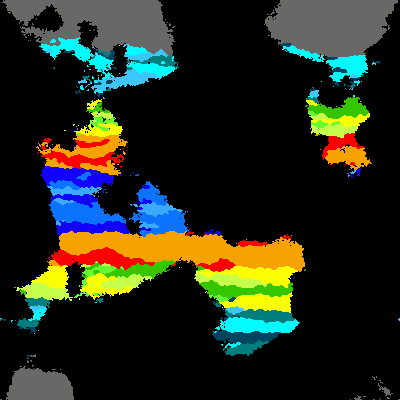
Since I intend to use this as a terrain generator, I want to be able to set the sea level, however I want to be able to set the sea level based on the percentage of land it will cover. It doesn't have to be exact, just fairly close.
What kind of analysis must I do on the pixels to determine how many of them fall below this arbitrary percentage? In other words, how do I find the height value that represents the nth percentile of the entire pixel population? I'm sure there is some really obvious answer but I am utterly failing to see it right now.
I know there are some math wonks around here so I'm hoping you guys can help me.
I have a program I'm working on that generates a heightmap using perlin noise. Straightforward stuff, right? For simplicity's sake, let's just say it creates an image of arbitrary size where each pixel has a value between 0 and 255, which is its height value.
Since I intend to use this as a terrain generator, I want to be able to set the sea level, however I want to be able to set the sea level based on the percentage of land it will cover. It doesn't have to be exact, just fairly close.
What kind of analysis must I do on the pixels to determine how many of them fall below this arbitrary percentage? In other words, how do I find the height value that represents the nth percentile of the entire pixel population? I'm sure there is some really obvious answer but I am utterly failing to see it right now.
I know there are some math wonks around here so I'm hoping you guys can help me.