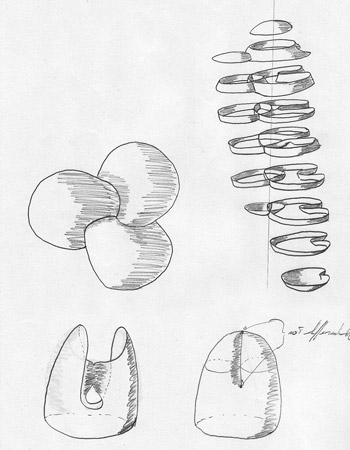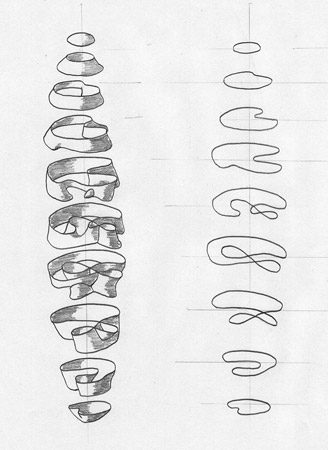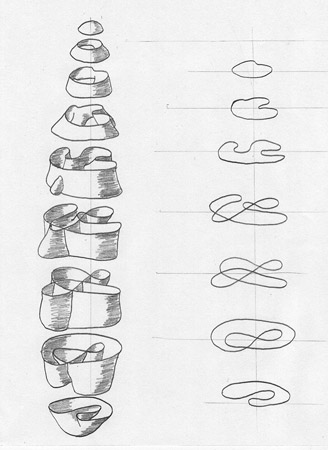non-Euclidean geometries

[Shaw]

I've been studying aspects of non-Euclidean geometries and topology since the late 1980s, and so it is sometimes hard for me to remember that most people aren't exposed to this stuff. And by most people, I'm including most people who major in math and physics too. These areas aren't pushed as mainstream topics even in math and physics, and are sometimes presented as being too hard for most people (even in those areas) to understand.

I, personally, think that with a little help these things can be understood... at least on a conceptual level. And a project was started back around 1990 to attempt to help people with visualizing this type of stuff. It started as an offshoot of the Minnesota Supercomputing Institute at the University of Minnesota called the Geometry Supercomputer Project. This was later given additional funding by the National Science foundation and the Department of Energy to form the Geometry Center.

My connection with the Geometry Center was rather limited... I did research there in the summer of 1994 on the topic of tight immersions of manifolds while I was a student at UCSD. I had the odd distinction of being the only person there that summer doing research that didn't make use of the computer systems at the center (about 8 SGIs, 12 Suns, 30 NeXTs, and 25 Macs) for my research.

But the Geometry Center put out some great stuff that was design to be approachable by everyone. A couple of these projects included video productions, which I think might be interesting for some of the people here. And thankfully even after NSF pulled it's funding, University of Illinois Urbana-Champaign took up the cause of hosting (most) of the Geometry Center's web site (which was one of the first sites on the web when it started).

Starting points...

Not Knot (1990)
This video is currently up on YouTube. You can find part one here and part two here. Additional information (including stills) can be found here.

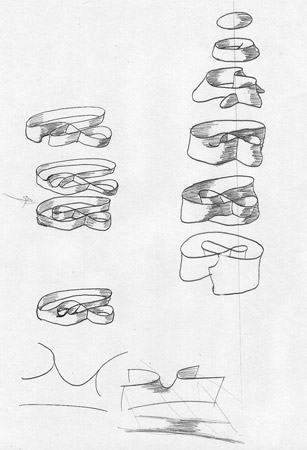
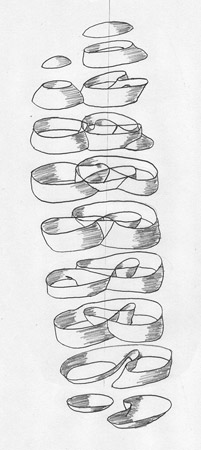
Outside In (1994)
This video is also currently up on YouTube. You can find part one here and part two here. Additional information (including stills) can be found here. This video covers a topic close to the type of stuff I was researching in differential topology which included the study of immersions of manifolds and homotopy theory. As I recall, this video won some awards at SIGGRAPH and was made using a combination of Geomview, Mathematica and Renderman using an SGI Crimson RE (which was the highest end computer we had there back in 1994). Geomview was an application developed at the Geometry Center and originally only ran on SGI and NeXT systems (and I still run this app on my SGI and NeXT systems today).

Geometry and the Imagination (1991)
This was a course designed to introduce people (mainly teachers and math students) to some of the more interesting aspects of mathematics which you wouldn't normally see early on in a math education. You can find the original course materials here, and a more recent version here (pdf).​

Hopefully this stuff will be both interesting and enjoyable for some of you guys.

 

[Shaw]

Someone recently was asking about the type of mathematics I specialized in and while it is one thing to tell someone about the mathematics I enjoy, this really is more of a visual area and should be seen. Usually when I an attempting to visualize surfaces immersed in three-space I work through quite a bit of scratch work first before I attempt to draw the full surface. Those notes tend to look like this...

Click to enlarge​

Which in turns starts developing into sketches like this...

Click to enlarge​

And this...

Click to enlarge​

And generally end up looking like these...

Click to enlarge


Click to enlarge


Click to enlarge​

All three of which are actually the same surface (deformed via regular homotopy), the Real Projective Plane (which is a great surface this type of mental exercise).

By this point you may have noticed that all of this has been done using the high tech tools of pencil and paper. Yes, there are programs that can create similar shapes, and I have a few of those... including Mathematica, LiveMath Maker and 3D-XplorMath (and here).

But here is the thing, the goal in drawing these wasn't to make the images, the goal was to make sure that I had a full and complete 3D representation of what was happening with that surface in my head. And to hand draw something like this, you have to really know the surface as it is completely a construct of the mind. If the computer does all this for you (as is becoming the case more and more these days), then one becomes an observer of this rather than an active participant.

Anyways, just thought I would share them with you guys.

 

[FlyingLemons]

Fascinating representation of deformation of surfaces - I'd thought about surfaces before in my topology classes, but never actually tried to visualize the process of deforming a surface outside of mathematics.

That said, I didn't spend most of my time thinking about the concepts in pure math - the topology was merely there to get my head around the notion of spaces and manifolds for general relativity and string theory. I've always found topology an enjoyable subject to work on. Maybe I might again some day...

Thanks for sharing this.

 

[Shaw]

I started out as a physics major, but after taking both the under graduate and graduate series in differential geometry to have a better foundation for general relativity, I realized I just liked mathematics more. Though I never thought about topology for general relativity, differential topology and homotopy theory (which is the area these images were drawn for) can be quite helpful. One of my favorite physics books is Techniques of Differential Topology in Relativity by Penrose.

Sadly, most of the physicist I've met got so caught up in the math of general relativity that they miss what it is. I don't know much about string theory, but enjoyed studying gauge theories (which is pretty much connections over fiber bundles with Lie group structures). From what I've read about string theory, it wants to treat gravity like a force, which leaves them with a messy time issue.

But yeah, the techniques I've used here for the smooth immersions of a non-orientable two-surface into euclidean three-space is a great way to build up one's visualization abilities for dealing with imbeddings and immersions (both smooth and simplicial) of n manifolds into n+m euclidean space. I got started working with this back in 1994 when doing research on tight immersions of surfaces.

I've found that sitting down with a pencil and paper (and a lot of time) and constructing multiple illustrations of the Real Projective Plane (RP2) from memory makes for a good mental exercise. The starting point isn't that big a deal as there are only four basic contour diagrams for RP2 (all having three cusps and all deformable into one another via regular homotopy). From there it is just a matter of reconstructing the surface around the fold curves and determining level sections (I use a technique that is sort of the reverse of my professor's for this) and putting it all together.



Yeah, beyond pencil and paper, the only other resources I generally require are aspirin and water.

 

[FlyingLemons]

Topology actually is a current topic in cosmology - some believe that the universe has a non-trivial topology that we might be able to see through observations of the cosmic microwave background.

There's also an idea that noncommutative geometry might have an impact on the early universe as well, with some trying to find a motivation for various models of inflation from it. And also string theory has some ideas about the inflationary period being powered by moduli fields which arise from "holes" in various spaces, or at least that's what it appeared to be. I never actually read too much about strings...

But topology is definitely becoming very important in theoretical physics today, which I'm quite glad of.

 

[think]

I hope it is not a problem to open this thread up again ... today but anyway you seem like you might be able to map this as a possible non-euclidean geometry ?

Background-when I was younger - I tried to solve the Fermat problem using x cubed plus y cubed plus z cubed equaling the distance to x,y,z ... cubed or r cubed this was not a euclidean type space and I was distraught but even still these cubes have whole number values for x,y,z, and r say x-3, y-4, z-5, r-6 for instance., that solve this equation ., would you Shaw who can draw such spaces in paper take this problem of sketching this - at your leisure? x^3+y^3+z^3=r^3

Bill,

 

[Shaw]

I hope it is not a problem to open this thread up again ... today but anyway you seem like you might be able to map this as a possible non-euclidean geometry ?

Background-when I was younger - I tried to solve the Fermat problem using x cubed plus y cubed plus z cubed equaling the distance to x,y,z ... cubed or r cubed this was not a euclidean type space and I was distraught but even still these cubes have whole number values for x,y,z, and r say x-3, y-4, z-5, r-6 for instance., that solve this equation ., would you Shaw who can draw such spaces in paper take this problem of sketching this - at your leisure? x^3+y^3+z^3=r^3

Bill,

Okay, lets take a quick look at this for a minute... usually when I'm doing a drawing it would be a mapping of some n manifold back into an n+m Euclidean space, and that is mainly done to look at the topological implications... to help with visualizing (or sharing a visualization) of what is being studied. Most drawings are 2 manifolds mapped back into Euclidean 3 space.

In this case, we'd first need to nail down the geometry of the topological space you want to visualize... and looking at the equation you are putting forward, the best way to do that is by reverse engineering a metric for what looks like a 3-manifold (and that is assuming that your "r" is a distance/radius like variable). The other thing to consider is the overall curvature of the 3-manifold (positive, negative or flat), which can be telling, and if it includes things like handles (which is a much harder thing to nail down with manifolds of more than 2 dimensions).

All that having been said... is it possible, maybe. But it doesn't look in any way trivial to crunch through, and even with that structure in hand it wouldn't lend itself to an easy way to visualize what it'd be like.


That is a really quick-n-dirty assessment. Someone with more time to devote to this might be able to take it much further. If you wanted to attempt it on your own, those are some of the things you might want to look into while studying it.

 

[sojourner]

Dude, 6 year old thread?

 

[{ Emilia }]

Certainly not!

It'd be nice if people hit "notify" instead of adding even more useless comments to an old thread, though.

 

[{ Emilia }]

Tentatively reopening this thread since there might actually be a demand.
Don't make me regret it by turning the magical resurrection of old threads into a habit.

 

[CorporalCaptain]

Since it really belongs here, reposted from N-space and M-space expressions:

With respect to think's question concerning non-Euclidean geometry, and regarding the equation x^3+y^3+z^3=r^3:

1) When using that equation to define distance in three-dimensional space, the resulting norm is classified as a p-norm with p=3 (p=3 coming from the third power, not the three dimensions). Wikipedia article on L^p spaces.

2) Because x^3+y^3+z^3 is not a quadratic form, metric spaces defined using the p-norm with p=3 are not Riemannian spaces. So, that well-known flavor of non-Euclidean geometry is out of the picture, and you're looking at something that is not as widely applied.

3) With respect to drawing things in the space, such as unit spheres, there are examples on the wiki page of unit circles (in two dimensions) for a few different values of p, but unfortunately not p=3. This person was kind enough to have drawn a unit circle for p=3 (you can see the progression of circles for p=1,2,3,4 already clearly approaching the axis-aligned square for p=infinity).

4) As an addendum to the reposted post, point (3), the unit circle in L^p space is called a superellipse. The superellipse article at MathWorld also has pictures.

 

[think]

The idea I was playing with was not for mapping in a non-Euclidean space which can be, but for creating a kind of new number theory of whole numbers that would solve the Fermat problem,.. I will work on the maths behind this number theory today... as I might have time if I drop the reality mapping notes... for a moment or two.

~Bill = peace.