The Nature of the Universe, Time Travel and More...

[Will The Serious]

How? Math I assume

It's the math that gave us the question of "dark matter". The math says there's more than we see. The math is based on observations combined with theories and when we consider new truths, we look to the math to confirm them, but our math tells us there's something out there that we don't see. The math might even tell us where to look and what effects to look for, but what the math doesn't tell us is what that thing we are looking for is. If we assume the space between visible bodies is empty, then our math says there are other bodies out there we can't see. However, if we don't assume the space between bodies is empty, then the math can be satisfied. We still know nothing about what we're looking for.

What we need is some way of actually seeing the water we are swimming in. An æther could satisfy these math equations, but then other math equations would be left unsatisfied. Maybe those unsatisfied math equations just need a new concept of the nature of the æther.

However, even if we do come up with a concept of reality that satisfies the math, without physical knowledge of the thing, it is still based on faith that we are looking at it the right way.

-Will

 

[publiusr]

Again, more talk about new physics

New physics needed? Experts suggest possibility of updating fundamental physics concepts

An unexpected finding about how our universe formed is again raising the question: do we need new physics? The answer could fundamentally change what physics students are taught in classes around the world.

phys.org

Look’s like we’re in solitary

Astronomers say we may live at the center of a cosmic void 2 billion light-years wide that defies the laws of cosmology

If this gigantic cosmic void does exist, it could help astronomers solve one of the greatest mysteries of our universe.

www.businessinsider.com

 

[Will The Serious]

It will likely take years to know which of the researchers' theories is correct. But the study gives a blueprint for future research.
https://phys.org/news/2024-09-physics-experts-possibility-fundamental-concepts.amp

As it should. We will probably never know which one is correct, but we can probably know which ones are incorrect, at some point.

While Relativity and Quantum physics are still in their Theoretical stage, the fundamental Laws of Motion and Thermodynamics seem pretty foundational. If we ever decide something can be created from nothing, I would question the nature of Nothing science thinks something could come from.

-Will

 

[Will The Serious]

What is "Dark Energy"? Another construct to fill in the gaps. But what does it have to do with intelligent life?

https://astrobiology.com/2024/11/a-...he-chances-of-intelligent-life-elsewhere.html

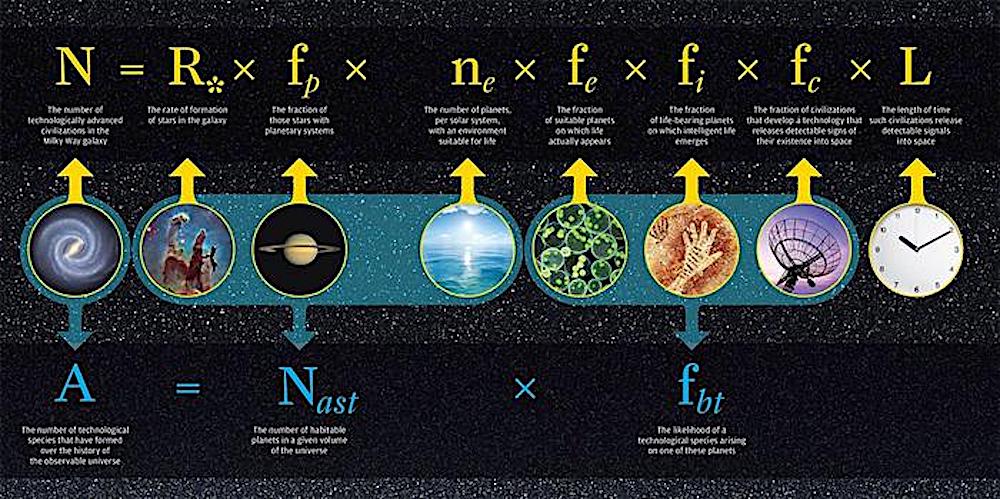
"The chances of intelligent life emerging in our Universe – and in any hypothetical ones beyond it – can be estimated by a new theoretical model which has echoes of the famous Drake Equation.
...
What is the calculation?

Since stars are a precondition for the emergence of life as we know it, the model could therefore be used to estimate the probability of generating intelligent life in our Universe, and in a multiverse scenario of hypothetical different universes.
...
It concludes that a typical observer would expect to experience a substantially larger density of dark energy than is seen in our own Universe – suggesting the ingredients it possesses make it a rare and unusual case in the multiverse."

The Drake Equation, a mathematical formula for the probability of finding life or advanced civilisations in the Universe...

"The approach presented in the paper involves calculating the fraction of ordinary matter converted into stars over the entire history of the Universe, for different dark energy densities.

The model predicts this fraction would be approximately 27 per cent in a universe that is most efficient at forming stars, compared to 23 per cent in our own Universe."

Does this research suggest that we might do better finding intelligent life by looking outside our own Universe?

I haven't really touched upon the concept of Dark Energy yet. Dark Matter may be the source of Dark Energy, or a consequence? I'm curious about the forces behind diffusion and I can't help but wonder if Dark Energy can be explained by the absence of matter.

Could there be a 'matter edge' to our Universe across which matter is compelled to go, to fill the space. I'm referring to True Space, where there really is nothing. Between our stars, there is matter, spread out and depressurized as it must be. Water boils into water vapor in space and becomes an expanded, depressurized gas. Every other gas must act in the same way. It diffuses into space, filling it. But what about at the distant edge, where the energy from the Big Bang hasn't reached? Could that space be calling to the matter to fill it? Might that be a force or would that be the untangled, un-bent space before matter forces a gravitational structure upon it? The gravitational structures in space/time call to each other, merging those structures into denser and denser wrinkles of space, but what does unwrinkled space do to wrinkled space?

Place a swatch of material on a table, such as a linen table napkin. Smooth it out flat but put a small wrinkle or bump in the cloth. Just a little hump of extra material. Pretend, or theorize, whichever makes you feel better, that that hump of extra material that rises slightly above the smooth plane of the table napkin is a bit of matter and the warp and woof of the cloth are the distortions of space that result.

Now for the "magic" of cosmological science. Without letting the edges of the cloth move, press out the wrinkle gently with a finger.

What you should observe is a new and nearly exact wrinkle forming somewhere else in the cloth. It forms at the exact same time that the original wrinkle disappears. You can push the wrinkle around too, roll that wrinkle across the Universe of the cloth with a finger. It never looses mass, it's form remains very similar except for the distortions of the manipulating finger. This could be a theoretical model of matter emerging from the fabric of the Universe.

Does my theoretical cloth and wrinkle experiment suggest a structure to the meta-cloth we see as our Universe? Maybe not, but perhaps it suggests a direction of inquiry.

The first experiment, I find the most intriguing, because if matter and the Universe can be described to act anything like the cloth on the table, that wrinkle can be made to travel instantaneously from one point to another, more distant, point without traversing any of the space in between.

‐Will

 

[Asbo Zaprudder]

Most intriguing is the idea that a straight line might be defined this way. I suggested such a definition in my Geometries class in college. Geometries was a class about non-Euclidean geometries. So straight lines have a slightly different meaning there.
Yes. I can see that.

Who are you quoting?

I'm interested in theories that treat space and time as emergent.

What Is Spacetime Really Made Of?

Spacetime may emerge from a more fundamental reality. Figuring out how could unlock the most urgent goal in physics—a quantum theory of gravity

www.scientificamerican.com

Whether my poor brain can grok such abstractions is doubtful.

 

[HIjol]

Who are you quoting?

I'm interested in theories that treat space and time as emergent.

What Is Spacetime Really Made Of?

Spacetime may emerge from a more fundamental reality. Figuring out how could unlock the most urgent goal in physics—a quantum theory of gravity

www.scientificamerican.com

Whether my poor brain can grok such abstractions is doubtful.

I think my brain is right next to yours, in this regard, but I so want to grok!

 

[Will The Serious]

Who are you quoting?

Myself.

My Geometries class was all about N-E geometry. In a presentation about curved space, I suggested that we could equate straight lines to distance over time (m/s, for example) and find the values that took the least time, to define the shortest distance (the straight line). This could also be converted mathematically to the least energy. In a universe of curved space, straight, as defined by the shortest distance between two points, takes on a distorted meaning, and measuring the shortest distance between two points becomes a matter of least resistance, or, in other words, the most efficient path for time and/or energy.

I drive long distances (up to 8 hours) to get to a fair where I sell my honey and jellies and spices. As above, when people ask how far away am I based, I use drive time, rather then distance to convey how far I've come. I live an hour from the Canadian border, I drove 3 hours to get here, My wife is at another show just half an hour away. The concept of converting one unit of measure to another through math is something we did in every section of our Physics course, back in the day. For practical application, it is pretty effective.

-Will

 

[Asbo Zaprudder]

I assume you're aware of the application of the stationary-action principle in physics.

The Einstein–Hilbert action in general relativity is the action that yields the Einstein field equations through the stationary-action principle.
...
Deriving equations of motion from an action has several advantages. First, it allows for easy unification of general relativity with other classical field theories (such as Maxwell's equations), which are also formulated in terms of an action. In the process, the derivation identifies a natural candidate for the source term coupling the metric to matter fields. Moreover, symmetries of the action allow for easy identification of conserved quantities through Noether's theorem.

Einstein–Hilbert action - Wikipedia

en.wikipedia.org

See also:

Action principles - Wikipedia

en.wikipedia.org

Lagrangian mechanics - Wikipedia

en.wikipedia.org

 

[Will The Serious]

From thee Wiki posted above:
"Newton's laws based on the concept of force, defined by the acceleration it causes when applied to mass: F=ma.

This approach to mechanics focuses on a single point in space and time, attempting to answer the question: "What happens next?".[3] Mechanics based on action principles begin with the concept of action, an energy tradeoff between kinetic energy and potential energy, defined by the physics of the problem. These approaches answer questions relating starting and ending points: Which trajectory will place a basketball in the hoop? If we launch a rocket to the Moon today, how can it land there in 5 days?[3] The Newtonian and action-principle forms are equivalent, and either one can solve the same problems, but selecting the appropriate form will make solutions much easier.

The energy function in the action principles is not the total energy (conserved in an isolated system), but the Lagrangian, the difference between kinetic and potential energy. The kinetic energy combines the energy of motion for all the objects in the system; the potential energy depends upon the instantaneous position of the objects and drives the motion of the objects. The motion of the objects places them in new positions with new potential energy values, giving a new value for the Lagrangian.[4]: 125 

Using energy rather than force gives immediate advantages as a basis for mechanics. Force mechanics involves 3-dimensional vector calculus, with 3 space and 3 momentum coordinates for each object in the scenario; energy is a scalar magnitude combining information from all objects, giving an immediate simplification in many cases. The components of force vary with coordinate systems; the energy value is the same in all coordinate systems.[5]: xxv  Force requires an inertial frame of reference;[6]: 65  once velocities approach the speed of light, special relativity profoundly affects mechanics based on forces. In action principles, relativity merely requires a different Lagrangian: the principle itself is independent of coordinate systems.[7]"
https://en.m.wikipedia.org/wiki/Action_principles

"The energy function in the action principles is not the total energy (conserved in an isolated system), but the Lagrangian, the difference between kinetic and potential energy."
This is another concept I have been mulling over for the past few weeks. It seems to me that Newton's laws of motion can all be considered special case expressions of the law of Conservation of Energy. The difference between Newtonian physics and its expressions of Force, and the Lagrangian energy physics seems fundamentally to be the single point calculations that require a frame of reference because everything in math is about relationships. The single point doesn't do anything by itself. The two-point Lagrangian system has a built in frame of reference by virtue of relating the start point with the end point.

-Will

 

[Asbo Zaprudder]

Hard to tell which are quotes and which are comments. Did you watch the YouTube video? It's a great summary of the historical development of the stationary-action principle and explains why the Lagrangian is defined the way that it is. There's going to be a follow-up video from Veritasium, apparently. Hopefully, he'll also cover the Hamiltonian at some stage.

Meanwhile:

ETA: Another proposed (and more controversial) way of deriving physics is to use Fisher information:

This book defines and develops a unifying principle of physics, that of 'extreme physical information'. The information in question is, perhaps surprisingly, not Shannon or Boltzmann entropy but, rather, Fisher information, a simple concept little known to physicists. Both statistical and physical properties of Fisher information are developed. This information is shown to be a physical measure of disorder, sharing with entropy the property of monotonic change with time. The information concept is applied 'phenomenally' to derive most known physics, from statistical mechanics and thermodynamics to quantum mechanics, the Einstein field equations, and quantum gravity. Many new physical relations and concepts are developed, including new definitions of disorder, time and temperature. The information principle is based upon a new theory of measurement, one which incorporates the observer into the phenomenon that he/she observes. The 'request' for data creates the law that, ultimately, gives rise to the data. The observer creates his or her local reality.

Introduction (Chapter 0) - Physics from Fisher Information

Physics from Fisher Information - December 1998

www.cambridge.org

Can one peek behind the curtain and glimpse what gives rise to reality as we measure it? I have no idea.

 

[Will The Serious]

Did you watch the YouTube video? It's a great summary of the historical development of the stationary-action principle and explains why the Lagrangian is defined the way that it is.

Not yet. I try to familiarize myself with the basic concepts as you put them out for us, but I don't always get to them quickly.

Can one peek behind the curtain and glimpse what gives rise to reality as we measure it?

That is sort of the ultimate goal, right? I don't think it can be done, but we can approach that limit as we progress.

-Will

 

[Asbo Zaprudder]

Physics seems to have been stuck in a rut for decades - possibly due to incorrect conceptualisations and inadequate mathematics. I'm hoping that LLMs will provide new insights, but perhaps Stephen Wolfram is correct and we're bound by the limits set by computational irreducibility.

 

[publiusr]

Maybe Flammarion’s engraving had it right after all

 

[StarTrek1701]

Imagine if the scientific community deducted we are actually at the center of the universe and that old cultures had it right.

 

[Gingerbread Demon]

Imagine if the scientific community deducted we are actually at the center of the universe and that old cultures had it right.

In what way?

 

[publiusr]

If the universe is finite but boundless—everywhere you go is the “center.”

I hope Planet 9 is a black hole—a source of energy

Perhaps a fractal version of an un-illuminate room could be of use.

 

[Will The Serious]

Since the path of least action to fall from point  a to point  b due to gravity can be recreated with the use of a perfect circle rolling along, maybe Ptolemy got it right.

He just didn't realize the difference between a cycloid and an ellipses.

-Will

 

[Asbo Zaprudder]

Since the path of least action to fall from point  a to point  b due to gravity can be recreated with the use of a perfect circle rolling along, maybe Ptolemy got it right.

He just didn't realize the difference between a cycloid and an ellipses.

-Will

Well, Ptolemy' s model was incorrectly geocentric, as I hope we can agree. The ancient Greeks knew about conic sections and cycloids and the difference between them, but not about ordinary differential equations or even Newtonian mechanics, of course. The brachistochrone is the appropriate form of cycloid curve for fastest descent under a uniform gravitational field, which the Sun's (or Earth's) gravitation field is not except over short distances to a good approximation. Also, if a charged particle is subjected to uniform electric and magnetic fields perpendicular to one another, its trajectory is a cycloid. It is possible to derive Kepler's three laws of planetary motion using Lagrangian dynamics, provided one plugs in the appropriate form of the gravitational potential.

 

[Will The Serious]

Well, Ptolemy' s model was incorrectly geocentric, as I hope we can agree.

Yes, but amazing for that error alone. Imagine the complexity of the system that works to predict the celestial bodies' movements relative to Earth from that point of view.

The ancient Greeks knew about conic sections and cycloids and the difference between them

Absolutely. Apollonius of Perga wrote an extensive multi-volume treatise on Conics. It was reproduced by Hypatia about 600 years later. Ptolemy would have been familiar with Apollonius' work. The idea that the Sun is the center of the solar system is also older than Ptolemy.

Pythagoras was known to be the first to discover that the Evening Star and the Morning Star were both Venus.

Pythagoras knew the pentagonal path Venus made. And, as you say, the ancients were familiar with cycloids and conical sections. While it is very easy to believe that the connections were not made to deduce a heliocentric solar system, the ancients were obviously aware of all the clues.

but not about ordinary differential equations or even Newtonian mechanics, of course.

I'm not so sure. Yes, Newton and Leibniz invented Calculus, but there were some solutions that the ancients seemed to have known about that we can only image with the use of Calculus today. They new about infinitesimals (Zeno's Paradox, for example), and many of the precursor techniques such as Reimann sums. It is my guess that modern Calculus is simply the formalization and a small next-step in our mathematical advancement of the knowledge of those much more ancient than the 1700's.

But, politics, belief systems, and religion have always had their friction to add to the forces or action of progress in science.

Speaking of friction, how does the Principal of Least Action deal with the forces of friction on a falling object within a medium? Perhapse it simply treats non-gravitational and magnetic forces as independent from pure motion. Or is there a way of avoiding F=ma completely?

-Will

 

[Asbo Zaprudder]

Speaking of friction, how does the Principal of Least Action deal with the forces of friction on a falling object within a medium? Perhapse it simply treats non-gravitational and magnetic forces as independent from pure motion. Or is there a way of avoiding F=ma completely?

The videos I linked address those questions. The stationary-action principle* (the term least-action is somewhat misleading) can deal with non-gravitational fields such as the electomagnetic (EM) field.

There are techniques for dealing with dissipative and frictional effects, but sometimes it's easier to resort to Newtonian mechanics. The Lagrangian and Hamiltonian formulations are left to university courses, but school-level examination problems where friction is not involved would become much simpler if they were taught. However, I can understand that this would overload the syllabus.

* Note, it's principle, in any case, not principal.
'Principal' or 'Principle'? Advice from your pals at M-W