Gravitational Slingshot
Interplanetary space probes often make use of the "gravitational
slingshot" effect to propel them to high velocities. For example,
Voyager 2 performed a close flyby of Saturn on the 27th of August in
1981, which had the effect of slinging it toward its flyby of Uranus
on the 30th of January in 1986. Since gravity is a conservative
force, it may seem strange that an object can achieve a net gain in
speed due to a close encounter with a large gravitating mass. We
might imagine that the speed it gains while approaching the planet
would be lost when receeding from the planet. However, this is not
the case, as we can see from simple consideration of the kinetic
energy and momentum, which shows how a planet can transfer kinetic
energy to the spacecraft.
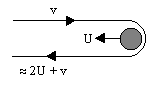
An extreme form of the maneuver would be to approach a planet
head-on at a speed v while the planet is moving directly toward
us at a speed U (both speeds defined relative to the "fixed" Solar
frame). If we aim just right we can loop around behind the planet
in an extremely eccentric hyperbolic orbit, making a virtual
180-degree turn, as illustrated below.
The net effect is almost as if we "bounced" off the front of the
planet. From the planet's perspective we approached at the speed
U+v, and therefore we will also receed at the speed U+v relative to
the planet, but the planet is still moving at (virtually) the speed
U, so we will be moving at speed 2U+v. This is just like a very
small billiard ball bouncing off a very large one.
To be a little more precise, conservation of kinetic energy and
momentum before and after the interaction requires
M U1^2 + m v1^2 = M U2^2 + m v2^2
M U1 - m v1 = M U2 + m v2
Eliminate U2 and solve for v2 to give the result
v2 = ((1-q)v1 + 2U1)/(1+q)
where q = m/M. Since q is virtually zero (the probe has negligible
mass compared with the planet), this reduces to our previous estimate of v2 = v1 + 2U1.